Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)Hai tam giác vuông \(\Delta AHC\approx\Delta BKC\)vì có chung góc nhọn C
b) Vì tam giác AHC đồng dạng tam giác BKC nên
\(\frac{AH}{BK}=\frac{HC}{KC}=\frac{AC}{BC}=\frac{4}{3}\)
Theo định lý Pytago ta có
\(AH=\sqrt{8^2-3^2}=\sqrt{55}\)
\(\frac{AH}{BK}=\frac{\sqrt{55}}{BK}=\frac{4}{3}\)
\(\Rightarrow BK=\frac{3\sqrt{55}}{4}\)
Theo Pytago ta có
\(KC=\sqrt{6^2-\left(\frac{3\sqrt{55}}{4}\right)^2}=\frac{9}{4}\left(cm\right)\)
\(KA=8-\frac{9}{4}=\frac{23}{4}\left(cm\right)\)

a) xét tam giác ABC và HAC có:
góc CAB=gócCHA=90độ
chung ACH
suy ra tam giác ABCđồng dạng với tam giác HAC
=> \(\frac{BC}{AC}=\frac{AC}{CH}=>AC^2=BC\cdot CH\)
b) vì tam giác ABC vuông tại A,áp dụng định lý pitago bạn sẽ tính được BC
thay vào \(\frac{BC}{AC}=\frac{AC}{CH}\)
bạn sẽ tính được CH,sau đó tương tự áp dụng pitago cho các tam giác còn lai là ra nhé
kết quả:HC=9,6;AH=7,2;BH=5,4

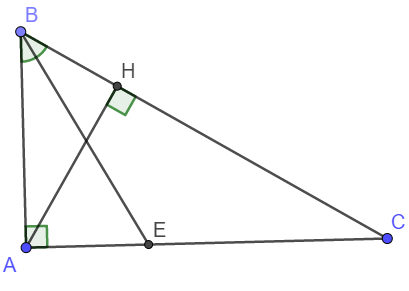
a) Xét tam giác ABC và tam giác HBA có:
\(\widehat{BAC}=\widehat{BHA}=90^o\)
Góc B chung
\(\Rightarrow\Delta ABC\sim\Delta HBA\left(g-g\right)\)
b)
Xét tam giác ABC và tam giác HAC có:
\(\widehat{BAC}=\widehat{AHC}=90^o\)
Góc C chung
\(\Rightarrow\Delta ABC\sim\Delta HAC\left(g-g\right)\)
c) Từ câu a và b ta có : \(\Delta HBA\sim\Delta HAC\)
\(\Rightarrow\frac{HB}{HA}=\frac{HA}{HC}\Rightarrow HA^2=HB.HC=9.16=144\)
\(\Rightarrow HA=12\left(cm\right)\)
Khi đó áp dụng định lý Pi-ta-go ta có:
\(AB^2=BH^2+AH^2=9^2+12^2\Rightarrow AB=15\left(cm\right)\)
\(AC^2=CH^2+AH^2=16^2+12^2\Rightarrow AC=20\left(cm\right)\)
BC = BH + HC = 9 + 16 = 25 (cm)
Áp dụng tính chất tia phân giác trong tam giác ta có:
\(\frac{AE}{EC}=\frac{AB}{BC}=\frac{15}{25}=\frac{3}{5}\)
\(\Rightarrow AE=\frac{3}{8}\times20=7,5\left(cm\right)\)
\(\Rightarrow EC=20-7,5=12,5\left(cm\right)\)

a) Ta có: AB^2 + AC^2 = 21^2 + 28^2 = 35^2 = BC^2
Vậy Tam giác ABC vuông tại A (đl Pytago đảo)
b) Ta có: Góc B + góc C = 90 độ (cmt câu a)
Góc HAC + góc C = 90 độ (Tam giác HAC vuông tại H)
=> Góc B = góc HAC
Mà Góc AHB= Góc AHC = 90 độ (Đường cao AH)
Vậy Tam giác HBA ~ tam giác HAC (góc - góc)
c)
Theo tính chất đường phân giác trong tam giác:
MB/ AB = MC / AC
<=> MB. AC = MC . AB
<=> MB . AC = (35- MB) . AB
<=> 35AB= MB.(AB+AC)
<=> MB = 35AB/(AB+AC) = 35.21/(21+28) = 15 cm
=> MC= 35 - 15 = 20 cm
Vậy MB = 15 cm, MC 20 cm
(Bạn tự vẽ hình và ghi giả thuyết kết luận nhé!)

a) Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABH}\) chung
Do đó: ΔABC\(\sim\)ΔHBA(g-g)
b) Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABH}\) chung
Do đó: ΔABC\(\sim\)ΔHBA(g-g)
hinh nhu ban chep sai de ban ve xem lai de di