Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Mx đi qua trung điểm M của BC và song song với AC. Suy ra Mx đi qua trung điểm E của AB (theo Định lí 1).
Tương tự, ta được F cũng là trung điểm của AC. Khi đó EF trở thành đường trung bình của tam giác ABC;
b) Do ME và MF cũng là đường trung bình nên có ME = MF = AE = AF. Suy ra AM là đường trung trực của EF.
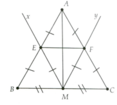

Mình không biết vẽ hình trên đây bạn tự vẽ hình nhé
Xét tam giác BAC có: BM=CM(M là trung điểm của BC)
ME//AC(Mx//AC)
=>AE=BE(hay E là trung điểm của AB)
Xét tam giác CBA có: BM=CM(M là trung điểm của BC)
MF//AB(My//AB)
=>AF=CF(hay F là trung điểm của AC)
Xét tam giác ABC có: AE=BE
AF=CF
=>EF là đường trung bình của tam giác ABC
b, Xét tứ giác AEMF có: ME//AF(Mx//AC)
MF//AE(My//AB)
=>AEMF là hình bình hành
Ta có: AE=BE; AF=CF
mà AB=AC(tam giác ABC cân tại A)
=>AE=BE=AF=CF
Xét hình bình hành AEMF có:AF=AE
=>AEMF là hình thoi
=> AM vuông góc với EF và AM đi qua trung điểm của EF
=>AM là đường trung trực của EF

a) Xét tam giác ABC có:
M là trung điểm BC(gt)
ME//AC(gt)
=> E là trung điểm AB
Xét tam giác ABC có:
M là trung điểm BC(gt)
MF//AB(gt)
=> F là trung điểm AC
Xét tam giác ABC có:
E là trung điểm AB(cmt)
F là trung điểm AC(cmt)
=> EF là đường trung bình
b) Xét tam giác ABC cân tại A có:
AM là đường trung tuyến(M là trung điểm BC)
=> AM là đường trung trực BC
=> AM⊥BC
Mà EF//BC(EF là đường trung bình)
=> EF⊥AM
Mà \(AE=AF=\dfrac{1}{2}AB=\dfrac{1}{2}AC\)
=> AM là đường trung trực EF

Bài 5:
Xét ΔEBC có
M là trung điểm của BC
I là trung điểm của EC
Do đó: MI là đường trung bình của ΔBEC
Suy ra: MI//DE
Xét ΔAMI có
D là trung điểm của AM
DE//MI
Do đó: E là trung điểm của AI
Suy ra: AE=EI
mà EI=IC
nên AE=EI=IC
Bài 4:
a: Xét ΔABC có
M là trung điểm của BC
ME//AC
Do đó: E là trung điểm của AB
Xét ΔABC có
M là trung điểm củaBC
MF//AB
Do đó: F là trung điểm của AC
Xét ΔABC có
E là trung điểm của AB
F là trung điểm của AC
Do đó: EF là đường trung bình của ΔBAC
b: Ta có: \(AE=EB=\dfrac{AB}{2}\)
\(AF=FC=\dfrac{AC}{2}\)
mà AB=AC
nên AE=EB=AF=FC
Xét ΔEBM và ΔFCM có
EB=FC
\(\widehat{B}=\widehat{C}\)
MB=MC
Do đó: ΔEBM=ΔFCM
Suy ra: ME=MF
Ta có: AE=AF
nên A nằm trên đường trung trực của EF(1)
Ta có: ME=MF
nên M nằm trên đường trung trực của EF(2)
từ (1) và (2) suy ra AM là đường trung trực của EF