Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(Bạn tự vẽ hình giùm)
Ta có \(\widehat{IBC}=\frac{\widehat{ABC}}{2}\)(BD là tia phân giác của \(\widehat{ABC}\))
và \(\widehat{ICB}=\frac{\widehat{ACB}}{2}\)(CE là tia phân giác của \(\widehat{ACB}\))
=> \(\widehat{IBC}+\widehat{ICB}=\frac{\widehat{ABC}+\widehat{ACB}}{2}\)
=> \(180^o-\widehat{BIC}=\frac{180^o-\widehat{A}}{2}\)
=> \(180^o-\widehat{BIC}=90^o-\frac{\widehat{A}}{2}\)
=> \(180^o-90^o=\widehat{BIC}-\frac{\widehat{A}}{2}\)
=> \(\widehat{BIC}-\frac{\widehat{A}}{2}=90^o\)
=> \(\widehat{BIC}=90^o+\frac{\widehat{A}}{2}\)
Thay \(\widehat{A}=80^o\)vào biểu thức \(\widehat{BIC}=90^o+\frac{\widehat{A}}{2}\), ta có:
\(\widehat{BIC}=90^o+\frac{80^o}{2}\)
=> \(\widehat{BIC}=90^o+40^o=130^o\)
Ta có ^IBC=^ABC2 (BD là tia phân giác của ^ABC)
và ^ICB=^ACB2 (CE là tia phân giác của ^ACB)
=> ^IBC+^ICB=^ABC+^ACB2
=> 180o−^BIC=180o−^A2
=> 180o−^BIC=90o−^A2
=> 180o−90o=^BIC−^A2
=> ^BIC−^A2 =90o
=> ^BIC=90o+^A2
Thay ^A=80ovào biểu thức ^BIC=90o+^A2 , ta có:
^BIC=90o+80o2
=> ^BIC=90o+40o=130o

Trong ΔBIC có: ∠(BIC) + ∠B1 + ∠C1 = 180o (tổng 3 góc trong tam giác)
Suy ra: ∠B1 + ∠C1 = 180o - ∠(BIC)
Ta có:
∠B1 = 1/2 ∠B (vì BD là tia phân giác)
∠C1 = 1/2 ∠C (vì CE là tia phân giác)
Suy ra: ∠B + ∠C = 2(∠B1 + ∠C1) = 2.(180o - ∠(BIC))
Trong ΔABC có: ∠A + ∠B + ∠C = 180o (tổng ba góc trong tam giác)
Suy ra: ∠A = 180o - (∠B + ∠C) = 180o - 2.(180o - ∠(BIC)) = 2. ∠(BIC) – 180o
∠(BIC) = 120o thì ∠A = 2.120o – 180o = 60o.


Trong tam giác ABC có:
∠A + ∠(ABC) + ∠(ACB) = 180o ⇒ ∠(ABC) + ∠(ACB) = 180o - 80o = 100o
Mà BI và CI lâ các tia phân giác nên
∠(ABC) + ∠(ACB) = 2.∠(IBC) + 2.∠(ICB) = 2 (∠(IBC) + ∠(ICB) )
Suy ra ∠(IBC) + ∠(ICB) = 50o
Mà ∠(IBC) + ∠(ICB) + ∠(BIC) = 180o ⇒ ∠(BIC) = 130o. Chọn C

Trong ΔBIC có: ∠(BIC) + ∠B1 + ∠C1 = 180o (tổng 3 góc trong tam giác)
Suy ra: ∠B1 + ∠C1 = 180o - ∠(BIC)
Ta có:
∠B1 = 1/2 ∠B (vì BD là tia phân giác)
∠C1 = 1/2 ∠C (vì CE là tia phân giác)
Suy ra: ∠B + ∠C = 2(∠B1 + ∠C1) = 2.(180o - ∠(BIC))
Trong ΔABC có: ∠A + ∠B + ∠C = 180o (tổng ba góc trong tam giác)
Suy ra: ∠A = 180o - (∠B + ∠C) = 180o - 2.(180o - ∠(BIC)) = 2. ∠(BIC) – 180o
∠(BIC) = α thì ∠A = 2.α – 180o.
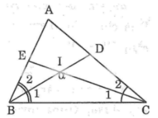

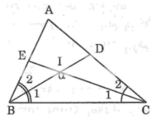
Xét ΔDBC vuông tại D và ΔECB vuông tại E có
BC chung
\(\widehat{DCB}=\widehat{EBC}\)
Do đó: ΔDBC=ΔECB
Suy ra: \(\widehat{IBC}=\widehat{ICB}\)
=>ΔICB cân tại I
=>\(\widehat{DBC}=\dfrac{180^0-110^0}{2}=35^0\)
\(\Leftrightarrow\widehat{ACB}=90^0-35^0=55^0\)
\(\Leftrightarrow\widehat{ABC}=55^0\)
hay \(\widehat{BAC}=70^0\)