K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

12 tháng 12 2016
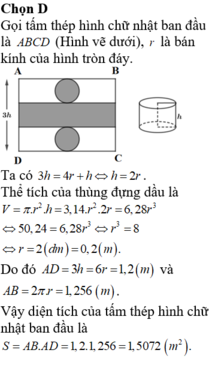
Giải
đàu tiên ta tìm bán kính đường tròn ngoại tiếp tam giác cân ABE (EA=EB)
R=\( \frac{AE.EB.AB}{4S}\) =\(\frac{5}{8}\) .Gọi I là tâm đường trong ngoại tiếp→AI=\(\frac{5}{8}\) .Gọi N là trung điểm SA
Trong mp(SAI) từ I kẻ đt d vuông góc vs đáy.Từ N kẻ đt vuông góc SA cắt d tại O
suy ra O là tâm mặt cầu cần tìm
dựa vào tam giác vuông OAI suy ra bán kính mặt cầu =\(\sqrt{OI^2 +AI^2}\)=\(\frac{\sqrt{41}}{8}\)
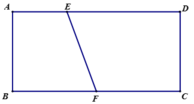
suy ra diện tích mặt cầu=4π\(R^2\) suy ra C

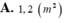
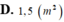
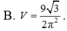

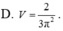



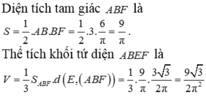




A B C D E F G H
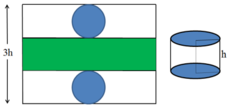
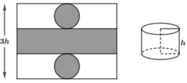
giả sử a=2 -> GC=1
AB=AC=\(\sqrt{2}\)
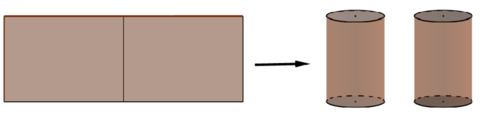
Đặt DE=x FE=x/2
Theo Talet trong tam giác AGC có
\(\dfrac{FE}{GC}=\dfrac{AE}{AC}\) có AC=\(\sqrt{2}\) FE= x/2 GC=1
suy ra AE=\(\dfrac{x\sqrt{2}}{2}\) suy ra EC= \(\sqrt{2}-\dfrac{x\sqrt{2}}{2}\)
Tính được HC = GC-GH=1-x/2
Trong tam giác EHC theo pytago có :
EH2=EC2-HC2 suy ra EH2=(2-2x+x2/2)-(1-x+x2/4)
EH^2= x^2/4-x+1=(x/2-1)^2
suy ra EH=(1-x/2) (do x< 2 khi phá dấu trị tuyệt đối lấy dấu trừ)
Vậy diện tích xq hình trụ cần tìm là 2pi nhân EH nhân DE/2
vậy để diện tích xq hình trụ min cũng có nghĩa là EH nhân DE/2 min hay (1-x/2) nhân x/2 min
-> TÌm GTNN của S=x/2-x^2/4
dễ thấy giá trị của x cần tìm là 1
Vậy với x =1 thì diện tích xq hình trụ min và khi đó diện tích hcn là 1 x (1-1/2)=1/2
Do ta giả sử a=2 nên giá trị cần tìm là a^2/8 (với a=2 thì a^2/8 = 1/2)
Do ABC vuông cân nên EHC cũng vuông cân, vậy thu gọn bớt rồi