Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta thấy : \(\left\{{}\begin{matrix}\Sigma\overrightarrow{P_t}=m_1.\overrightarrow{v_1}+m_2\overrightarrow{v_2}=0,5\overrightarrow{v_1}+0,3\overrightarrow{v_2}\\\Sigma\overrightarrow{P_s}=\left(m_1+m_2\right)\overrightarrow{v}=0,8\overrightarrow{v}\end{matrix}\right.\)
- Áp dụng định luật bảo toàn động lượng ta được :
\(0,8\overrightarrow{v}=0,5\overrightarrow{v_1}+0,3\overrightarrow{v_2}\)
Mà \(v,v_1,v_2\) cùng hướng .
\(\Rightarrow0,5v_1+0,3v_2=0,8v\)
\(\Rightarrow v=\dfrac{0,5v_1+0,3v_2}{0,8}=\dfrac{0,5.4+0,3.0}{0,8}=2,5\left(m/s\right)\)
Vậy ...

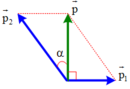
Khi đạn nổ bỏ qua sức cản của không khí nên được coi như là một hệ kín.
Theo định luật bảo toàn động lượng: p → = p → 1 + p → 2
+ Với p = m v = 2.250 = 500 k g . m / s p 1 = m 1 v 1 = 1.500 = 500 k g . m / s p 2 = m 2 v 2 = v 2 k g . m / s
+ Vì v → 1 ⊥ v → 2 ⇒ p → 1 ⊥ p → theo pitago
⇒ p 2 2 = p 1 2 + p 2 ⇒ p 2 = p 1 2 + p 2 = 500 2 + 500 2 = 500 2 k g m / s
+ Mà sin α = p 1 p 2 = 500 500 2 = 2 2 ⇒ α = 45 0
Vậy mảnh hai chuyển động theo phương hợp với phương thẳng đứng một góc 45 ° với vận tốc 500 2 m / s (m/s)
Chọn đáp án A

Khi đạn nổ bỏ qua sức cản của không khí nên được coi như là một hệ kín.
Theo định luật bảo toàn động lượng p → = p → 1 + p → 2
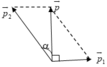
Với p = m v = 2.250 = 500 ( k g m / s ) p 1 = m 1 v 1 = 1.500 = 500 ( k g m / s ) p 2 = m 2 v 2 = v 2 ( k g m / s )
Vì
v → 1 ⊥ v → ⇒ p → 1 ⊥ p → t h e o p i t a g o ⇒ p 2 2 = p 1 2 + P 2 ⇒ p 2 = p 1 2 + p 2 = 500 2 + 500 2 = 500 2 ( k g m / s )
⇒ v 2 = p 2 = 500 2 ( m / s ) M à sin α = p 1 p 2 = 500 500 2 = 2 2 ⇒ α = 45 0
Vậy mảnh hai chuyển động theo phương hợp với phương thẳng đứng một góc 45 0 với vận tốc 500 2 ( m / s )

Áp dụng định luật hai Newton lên vật m1
\(\overrightarrow{F_1}+\overrightarrow{N_1}+\overrightarrow{P_1}=m_1\overrightarrow{a_1}\)
\(\Rightarrow F_1=m_1a_1\)
Áp dụng định luật hai Newton lên vật m2
\(\overrightarrow{F_2}+\overrightarrow{N_2}+\overrightarrow{P_2}=m_2\overrightarrow{a_2}\)
\(\Rightarrow F_2=m_2a_2\)
Lại có: \(F_1=F_2\Rightarrow m_1a_1=m_2a_2\)
Mà \(a=\dfrac{2s}{t^2}\)
\(\Rightarrow m_1s_1=m_2s_2\)
\(\Leftrightarrow m_1=3m_2\) (1)
Có: \(m_1+m_2=3\) (2)
Từ (1) và (2) giải hệ phương trình ta được: \(\left\{{}\begin{matrix}m_1=3\left(kg\right)\\m_2=1\left(kg\right)\end{matrix}\right.\)

Các vận động viên khi bơi tới mép hồ bơi và quay lại thì dùng chân đẩy mạnh vào vách hồ bơi để đi chuyển nhanh hơn là vì khi VĐV tác dụng lực vào vách hồ bơi thì vách hồ bơi cũng sẽ tác dụng một lực lên chân của VĐV. Lực này giúp cho các VĐV có đà và di chuyển nhanh hơn.

Lò xo bị nén rồi lại buông tay nên \(\overrightarrow{F_1}=-\overrightarrow{F_2}\).
\(\Rightarrow F_1=F_2\Rightarrow m_1\cdot a_1=m_2\cdot a_2\Rightarrow\dfrac{m_1}{m_2}=\dfrac{a_2}{a_1}\)
Mặt khác: \(S=\dfrac{1}{2}at^2\Rightarrow a=\dfrac{2S}{t^2}\)
Từ đó: \(\dfrac{m_1}{m_2}=\dfrac{a_2}{a_1}=\dfrac{\dfrac{2S_2}{t^2}}{\dfrac{2S_1}{t^2}}=\dfrac{S_2}{S_1}=\dfrac{6}{2}=3\)
\(\Rightarrow m_1=3m_2=3\cdot2=6kg\)
Chọn A.

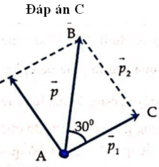
- Xét hệ gồm hai mảnh đạn trong thời gian nổ, đây là hệ kín nên ta áp dụng định luật bảo toàn động lượng ta được
- Động lượng trước khi đạn nổ:
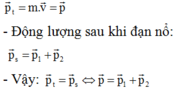
- Từ hình áp dụng định lý hàm số sin cho ![]() tạo bởi 3 cạnh là động lượng tương ứng của p, p1, p2 ta
tạo bởi 3 cạnh là động lượng tương ứng của p, p1, p2 ta
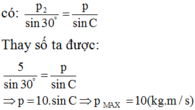

Đáp án C
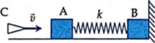
- Để B có thể dịch sang trái thì lò xo phải giãn một đoạn ít nhất là x0 sao cho:
![]()
![]()
- Như thế, vận tốc v0 mà hệ (m1 + m) có được ngay sau khi va chạm phải làm cho lò xo có độ co tối đa x sao cho khi nó dãn ra thì độ dãn tối thiểu phải là x0

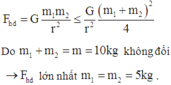
Trả lời:
Vì sau khi bẻ đôi viên thuốc. Các liên kết giữa hai mảnh đã bị phá vỡ. Khi ép sát hai mảnh, khoảng cách giữa các phân tử trong hai mảnh lớn hơn kích thước phân tử thuốc nên lực tương tác giữa các phân tử trong hai mảnh là không đáng kể. Do đó, hai mảnh không thể dính liền với nhau.