Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: AB = AD (gt) => A thuộc đường trung trực của BD
CB = CD (gt) => C thuộc đường trung trực của BD.
Vậy AC là đường trung trực của BD.
b) Xét ∆ ABC và ∆ADC có AB = AD (gt)
nên ∆ ABC = ∆ADC (c.c.c)
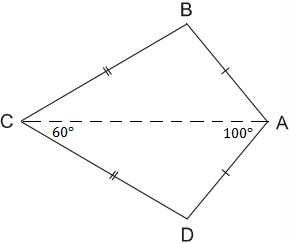
Suy ra: ⇒ˆB=ˆD
Ta có ˆB+ˆD=3600–(100+60)=200
Do đó ˆB=ˆD=1000

a) ta thấy ab = ab ; bc = cd
=> tứ giác ABCD là hình bình hành
=> AC và BD cắt nhau tai trung điểm của mỗi đường
=> AC là đường trung trực của BD
b) Ta có A + D = 180
=> D = 180 - 100
=> D= 80
Ta lại có B + C = 180
=> C = 180 - 60
=> C = 120

a) Ta có:
AB = AD (gt) ⇒ A thuộc đường trung trực của BD
CB = CD (gt) ⇒ C thuộc đường trung trực của BD
Vậy AC là đường trung trực của BD
b) Xét ΔABC và ΔADC có:
AB = AD (gt)
BC = DC (gt)
AC cạnh chung
⇒ ΔABC = ΔADC (c.c.c)
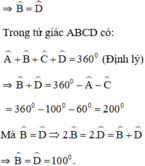

a) Ta có: AB = AD (gt) => A thuộc đường trung trực của BD
CB = CD (gt) => C thuộc đường trung trực của BD.
Vậy AC là đường trung trực của BD.
b) Xét ∆ ABC và ∆ADC có AB = AD (gt)
BC = DC (gt)
AC cạnh chung
nên ∆ ABC = ∆ADC (c.c.c)

Suy ra: ⇒ \(\widehat{B}=\widehat{D}\)
Ta có \(\widehat{B}+\widehat{D}=360^o-\left(100^o+60^o\right)=200^o\)
Do đó \(\widehat{B}=\widehat{D}=100^o\)
Bài giải:
a) Ta có: AB = AD (gt) => A thuộc đường trung trực của BD
CB = CD (gt) => C thuộc đường trung trực của BD.
Vậy AC là đường trung trực của BD.
b) Xét ∆ ABC và ∆ADC có AB = AD (gt)
BC = DC (gt)
AC cạnh chung
nên ∆ ABC = ∆ADC (c.c.c)

Suy ra: ⇒ˆB=ˆD⇒B^=D^
Ta có ˆB+ˆD=3600−(100+60)=200B^+D^=3600−(100+60)=200
Do đó ˆB=ˆD=1000B^=D^=1000

Bài 4:
Xét ΔAED vuông tại E và ΔBFC vuông tại F có
AD=BC
góc D=góc C
Do đó: ΔAED=ΔBFC
=>DE=CF
Bài 3:
a: Xét ΔADC và ΔBCD có
AD=BC
AC=BD
DC chung
Do đó: ΔADC=ΔBCD
=>góc ACD=góc BDC
b: Ta co: góc ACD=góc BDC
=>góc EAB=góc EBA
=>ΔEAB cân tại E

Bài 1)
a) Vì A: B:C:D = 1:2:3:4
=> A= B/2 = C/3=D/4
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
A = 36 độ
B= 72 độ
C=108 độ
D= 144 độ
b) Ta có :
A + D = 36 + 144 = 180 độ(1)
B+C = 72 + 108 = 180 độ(2)
Từ (1) và (2) ta có:
=> AB //CD (dpcm)
c) Ta có :
CDE + ADC = 180 độ(kề bù)
=> CDE = 180 - 144 = 36
Ta có :
BCD + DCE = 180 độ ( kề bù)
=> DCE = 180 - 108 = 72
Xét ∆CDE ta có :
CDE + DCE + DEC = 180 ( tổng 3 góc trong ∆)
=> DEC = 180 - 72 - 36 = 72 độ
Bài 2)
a) Ta có ABCD có :
A + B + C + D = 360 độ
Mà C = 80 độ
D= 70 độ
=> A+ B = 360 - 80 - 70 = 210 độ
Ta có AI là pg góc A
BI là pg góc B
=> DAI = BAI = A/2
=> ABI = CBI = B/2
=> BAI + ABI = A + B /2
=> BAI + ABI = 210/2 = 105
Xét ∆IAB ta có :
IAB + ABI + AIB = 180 độ
=> AIB = 180 - 105
=> AIB = 75 độ
=>