Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
GTLN:
Áp dụng BĐT Cauchy-Schwarz:
\(B^2=(6\sqrt{x-1}+8\sqrt{3-x})^2\leq (6^2+8^2)(x-1+3-x)=200\)
\(\Rightarrow B_{\max}= 10\sqrt{2}\Leftrightarrow \frac{3}{\sqrt{x-1}}=\frac{4}{\sqrt{3-x}}\Leftrightarrow x=\frac{43}{25}\)
GTNN:
Ta biết một bổ đề sau: Với \(a,b\geq 0\Rightarrow \sqrt{a}+\sqrt{b}\geq \sqrt{a+b}\)
Cách CM rất đơn giản vì nó tương đương với \(\sqrt{ab}\geq 0\) (luôn đúng)
Áp dụng vào bài toán:
\(\Rightarrow B\geq \sqrt{36x-36+192-64x}=\sqrt{156-28x}\geq 6\sqrt{2}\) (do \(x\leq 3\))
Vậy \(B_{\min}=6\sqrt{2}\Leftrightarrow x=3\)


`10)`
Xếp `6` học sinh vào `7` chỗ là `2` lần hoán vị của `6`
`=>` Có `2.6!=1440` cách.
`11)` Chọn `3` học sinh trong `8` học sinh là chỉnh hợp chập `3` của `8`
`=>` Có `A_8 ^3=336` cách.
Xếp 6 học sinh vào 7 chỗ là 2 lần hoán vị của 6
⇒ Có 2.6≠1440 cách.
11) Chọn 33 học sinh trong 88 học sinh là chỉnh hợp chập 33 của 88
⇒ Có \(a\dfrac{3}{8}\)=336 cách.

`\Omega=C_38 ^3`
Gọi `A:`"Chọn `3` học sinh là nam."
`=>A=C_18 ^3`
`=>P(A)=[C_18 ^3]/[C_38 ^3]=68/703`
\(\Omega=c\dfrac{3}{28}\)
gọi a là chọn 3 học sinh là nam
a=\(c\dfrac{3}{18}\)
p(a)=\(\dfrac{c\dfrac{3}{18}}{c\dfrac{3}{38}}\)=\(\dfrac{68}{703}\)

4:
\(n\left(\Omega\right)=C^3_{35}\)
\(n\left(A\right)=C^3_{15}\)
=>\(P\left(A\right)=\dfrac{13}{187}\)

\(\left\{{}\begin{matrix}x=1+t\\y=2+2t\end{matrix}\right.\)
--->vtcp là \(\overrightarrow{u}\)=(1;2)


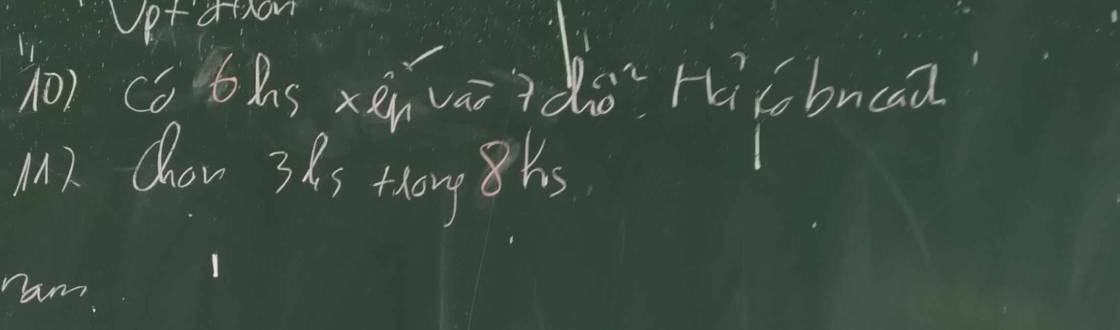
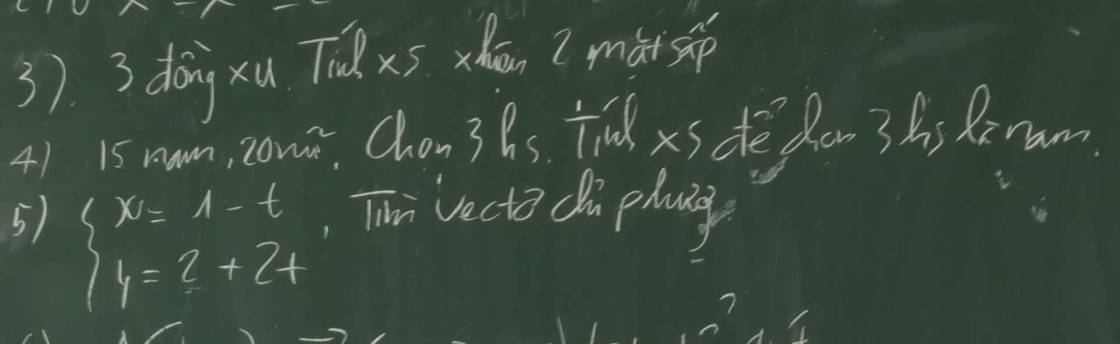

Dễ mà
Thế mà cx hỏi