Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left[{}\begin{matrix}x=2\sqrt{2}\simeq2.82\\x=-2\sqrt{2}\simeq-2.82\end{matrix}\right.\)

\(a)x^2=2\Rightarrow x_1=\sqrt{2}\) và \(x_2=-\sqrt{2}\)
Dùng máy tính bỏ túi ta tính được:
\(\sqrt{2}\text{≈}1,414213562\)
Kết quả làm tròn đến chữ số thập phân thứ ba là:
\(x_1=1,414;x_2=-1414\)
\(b)x^2=3\Rightarrow x_1=\sqrt{3}\)và \(x_2=-\sqrt{3}\)
Dùng máy tính ta được:
\(\sqrt{3}\text{≈ 1,732050907}\)
Vậy \(x_1=1,732;x_2=-1,732\)
\(c)x^2=3,5\Rightarrow x_1=\sqrt{3,5}\)và \(x_2=-\sqrt{3,5}\)
Dùng máy tính ta được:
\(\sqrt{3,5}\text{≈ 1,870828693}\)
Vậy \(x_1=1,871;x_2=-1,871\)
\(d)x^2=4,12\Rightarrow x_1=\sqrt{4,12}\)và \(x_2=-\sqrt{4,12}\)
Dùng máy tính ta được:
\(\sqrt{4,2}\text{≈ 2,029778313}\)
Vậy \(x_1=2,030;x_2=-2,030\)
a) x = \(\sqrt{2}\)
b) x = \(\sqrt{3}\)
c) x = \(\dfrac{\sqrt{14}}{2}\)
d)x = \(\dfrac{\sqrt{103}}{5}\)

\(\sin39^013'=0,6322\)
\(\cos52^018'=0,6115\)
\(\tan13^020'=0,2370\)
\(\cot10^017'=5,5118\)
\(\sin54^0=0,8090\)
\(\cos45^0=0,7071\)

giả sử góc a=135 độ , thì góc d=45 độ.kẻ đường cao ah khi đó góc dah=45 độ vậy tam giác adh cân và vuông.áp dụng pytago ah=6.căn bậc hai của 2.vậy diện tích hbh=15.6 căn bậc 2 của 2=90.căn bậc 2 của 2(cm^2)
vì ABCD là hình bình hành
=> AD // BC ( tính chất )
=> \(\widehat{A}+\widehat{B}=180^0\)( hai góc trong cùng phía)
=> \(\widehat{B}=180^0-110^0=70^0\)
Kẻ AH\(\perp\)BC tại H, ta có tam giác vuông ABH
Xét tam giác vuông ABH, có:
AH=AB*sin B=12*sin 70 độ
\(AH\approx11,276\)(cm)
ta có: AD=BC ( ABCD là hình chữ nhật )
\(\Rightarrow S_{ABCD}=AH\cdot BC\approx11,276\cdot15=169,14\)(\(cm^2\))

a) Ta có:
√4(1+6x+9x2)24(1+6x+9x2)2 =√4.√(1+6x+9x2)2=4.(1+6x+9x2)2
=√4.√(1+2.3x+32.x2)2=4.(1+2.3x+32.x2)2
=√22.√[12+2.3x+(3x)2]2=22.[12+2.3x+(3x)2]2
=2.√[(1+3x)2]2=2.[(1+3x)2]2
=2.∣∣(1+3x)2∣∣=2.|(1+3x)2|
=2(1+3x)2=2(1+3x)2.
(Vì (1+3x)2>0(1+3x)2>0 với mọi xx nên ∣∣(1+3x)2∣∣=(1+3x)2|(1+3x)2|=(1+3x)2)
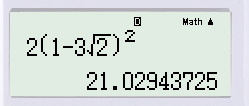
Thay x=−√2x=−2 vào biểu thức rút gọn trên, ta được:
2[1+3.(−√2)]2=2(1−3√2)22[1+3.(−2)]2=2(1−32)2.
Bấm máy tính, ta được: 2(1−3√2)2≈21,0292(1−32)2≈21,029.
b) Ta có:
√9a2(b2+4−4b)=√32.a2.(b2−4b+4)9a2(b2+4−4b)=32.a2.(b2−4b+4)
=√(3a)2.(b2−2.b.2+22)=(3a)2.(b2−2.b.2+22)
=√(3a)2.√(b−2)2=(3a)2.(b−2)2
=|3a|.|b−2|=|3a|.|b−2|
Thay a=−2a=−2 và b=−√3b=−3 vào biểu thức rút gọn trên, ta được:
|3.(−2)|.∣∣−√3−2∣∣=|−6|.∣∣−(√3+2)∣∣|3.(−2)|.|−3−2|=|−6|.|−(3+2)|
=6.(√3+2)=6√3+12=6.(3+2)=63+12.
Bấm máy tính, ta được: 6√3+12≈22,39263+12≈22,392.
a) Ta có:
√4(1+6x+9x2)2=√4.√(1+6x+9x2)24(1+6x+9x2)2=4.(1+6x+9x2)2
=√4.√(1+2.3x+32.x2)2=4.(1+2.3x+32.x2)2
=√22.√[12+2.3x+(3x)2]2=22.[12+2.3x+(3x)2]2
=2.√[(1+3x)2]2=2.[(1+3x)2]2
=2.|(1+3x)2|=2.|(1+3x)2|
=2(1+3x)2=2(1+3x)2.
(Vì (1+3x)2≥0(1+3x)2≥0 với mọi xx nên |(1+3x)2|=(1+3x)2|(1+3x)2|=(1+3x)2)
Thay x=−√2x=−2 vào biểu thức rút gọn trên, ta được:
2[1+3.(−√2)]2=2(1−3√2)22[1+3.(−2)]2=2(1−32)2.
Bấm máy tính, ta được: 2(1−3√2)22(1−32)2 ≈≈ 21,02921,029.
b) Ta có:
√9a2(b2+4−4b)=√32.a2.(b2−4b+4)9a2(b2+4−4b)=32.a2.(b2−4b+4)
=√(3a)2.(b2−2.b.2+22)=(3a)2.(b2−2.b.2+22)
=√(3a)2.(b−2)2=(3a)2.(b−2)2
=√(3a)2.√(b−2)2=(3a)2.(b−2)2
=|3a|.|b−2|=|3a|.|b−2|
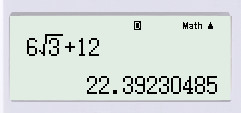
Thay a=−2a=−2 và b=−√3b=−3 vào biểu thức rút gọn trên, ta được:
|3.(−2)|.|−√3−2|=|−6|.|−√3−2||3.(−2)|.|−3−2|=|−6|.|−3−2|
=6.(√3+2)=6√3+12=6.(3+2)=63+12.
Bấm máy tính, ta được: 6√3+1263+12 ≈≈ 22,39222,392.

x^2+x-p=0 x^2+x=p x(x+1)=p mà p là số nguyên tố
x=1 và x+1=p p=2 thõa mãn đk thế vào trên tính được x1 và x2

Không có góc nhọn nào như vậy bởi nếu x là góc nhọn thì \(\sin x< =1;\cos x< =1\)