
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

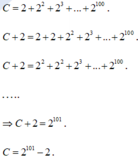

3n+2 - 2n+2 +3n - 2n = 3n . 32 - 2n. 22 +3n -2n
= 3n(32+1) - (2n.22 +2n)
=3n . 10 - 2n .5
=3n.10 - 2n-1 .2 .5
= 3n.10 - 2n-1 .10
= 10(3n - 2n-1)
vì 10 chia hết cho 10 nên 10(3n-2n-1) chia hết cho 10
=> 3n+2 - 2n+2 +3n -2n chia hết cho 10
Ai làm nhanh nhất mình sẽ **** xin cảm ơn các bạn mình đang cần gấp

Đặt \(D=2+2^2+2^3+...+2^{100}\)
\(\Leftrightarrow2D=2^2+2^3+2^4+...+2^{101}\)
\(\Leftrightarrow2D-D=D=2^{101}-1\)
\(\Rightarrow C=2^{101}-1-2^{108}\)

Ta có: \(A=\frac{1}{3}+\frac{2}{3^2}+\frac{3}{3^3}+...+\frac{100}{3^{100}}\)
\(\Rightarrow3A=1+\frac{2}{3}+\frac{3}{3^3}+...+\frac{100}{3^{99}}\)
\(\Rightarrow3A=1+\frac{1}{3}+\frac{1}{3}+\frac{2}{3^2}+\frac{1}{3^2}+...+\frac{99}{3^{99}}+\frac{1}{3^{99}}\)
\(\Rightarrow3A=\left(1+\frac{1}{3}+\frac{1}{3^2}+...+\frac{1}{3^{99}}\right)+\left(\frac{1}{3}+\frac{2}{3^2}+\frac{3}{3^3}+...+\frac{99}{3^{99}}\right)\)
\(\Rightarrow2A=B-\frac{100}{3^{100}}\) với \(B=1+\frac{1}{3}+\frac{1}{3^2}+...+\frac{1}{3^{99}}\)
Ta tính B:
\(B=1+\frac{1}{3}+\frac{1}{3^2}+...+\frac{1}{3^{99}}\)
\(\Rightarrow3B=3+1+\frac{1}{3}+...+\frac{1}{3^{98}}=3+B-\frac{1}{3^{99}}\)
\(\Rightarrow B=\frac{3}{2}-\frac{1}{2.3^{99}}\)
Vậy thì \(A=\frac{B}{2}-\frac{50}{3^{100}}\)
\(A=\frac{3}{4}-\frac{1}{4.3^{99}}-\frac{50}{3^{100}}=\frac{3^{101}-3-200}{4.3^{100}}=\frac{3^{101}-203}{4.3^{100}}\)

\(\frac{a_1}{a_2}=\frac{a_2}{a_3}=...=\frac{a_{100}}{a_1}=\frac{a_1+a_2+...+a_{100}}{a_1+a_2+...+a_{100}}=1\)\(\Rightarrow\)\(a_1=a_2=...=a_{100}\)
\(\Rightarrow\)\(M=\frac{a_1^2+a_2^2+a_3^2+...+a_{100}^2}{\left(a_1+a_2+a_3+...+a_{100}\right)^2}=\frac{100a_1^2}{100^2a_1^2}=\frac{1}{100}\)

S = 22 + 42 + 62 + ... + 202
S = 22 ( 12 + 22 + 32 + ... + 102 )
Vì 12 + 22 + 32 + ... + 102 = 385
=> S = 22 . 385
S = 4 . 385
S = 1540
Vậy S = 1540
Vì 2^2=2^2.1^2,4^2=2^2.2^2,....20^2=2^2.10^2
Suy ra S=2^2.(1^2+2^2+...+10^2)
Mà theo bài ra,phần dấu trong ngoặc bằng 385
Suy ra S=2^2.385=4.385=1540
Vậy S có giá trị bằng 1540

Bài 1:
Nếu a,b,c # 0 thì theo tính chất của dãy tỉ số bằng nhau , ta có:
\(\frac{a}{b+c}=\frac{b}{c+a}=\frac{c}{a+b}=\frac{a+b+c}{2\left(a+b+c\right)}=\frac{1}{2}\)
Nếu a + b + c = 0 thì b + c = -a ; c + a = - b ; a + b = -c
<=> Tỉ số của \(\frac{a}{b+c};\frac{c}{c+a};\frac{c}{a+b}\) Bằng -1