
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

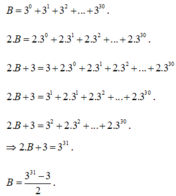

b)Ta có: \(\left(a-b\right)^2\ge0\)
\(\Leftrightarrow a^2-2ab+b^2\ge0\)
\(\Leftrightarrow a^2+b^2\ge2ab\)
\(\Leftrightarrow\frac{a^2}{ab}+\frac{b^2}{ab}\ge2\)
\(\Leftrightarrow\frac{1}{a}+\frac{1}{b}\ge2\left(đpcm\right)\)
\(a^5-a=a\left(a^4-1\right)\)
\(=a\left(a^2+1\right)\left(a^2-1\right)\)
\(=a\left(a^2+1\right)\left(a-1\right)\left(a+1\right)\)
\(=a\left(a^2-4+5\right)\left(a-1\right)\left(a+1\right)\)
\(=a\left(a^2-4\right)\left(a-1\right)\left(a+1\right)+5a\left(a+1\right)\left(a-1\right)\)
\(=\left(a-2\right)\left(a-1\right)a\left(a+1\right)\left(a+2\right)+5a\left(a+1\right)\left(a-1\right)\)
Tích 5 số nguyên liên tiếp chia hết cho 5 nên \(a^5-a⋮5\)

\(S=1+5+5^2+5^4+...+5^{200}\)
\(\Leftrightarrow5^2S=5^2+5^4+...+5^{202}\)
\(\Leftrightarrow25S=5^2+5^4+...+5^{202}\)
\(\Leftrightarrow25S-S=5^{202}-1\)
\(\Leftrightarrow S=\left(5^{202}-1\right)\div24\)
a) S = 1 + 52 + 54 + ... + 5200
=> 52S = 52.(1 + 52 + 54 + ... + 5200)
=> 25S = 52 + 54 + 56 + ... + 5202
=> 25S - S = (52 + 54 + 56 + ... + 5202) - (1 + 52 + 54 + ... + 5200)
=> 24S = 5202 - 1
=> S = \(\frac{5^{202}-1}{24}\)

3n+2 - 2n+2 +3n - 2n = 3n . 32 - 2n. 22 +3n -2n
= 3n(32+1) - (2n.22 +2n)
=3n . 10 - 2n .5
=3n.10 - 2n-1 .2 .5
= 3n.10 - 2n-1 .10
= 10(3n - 2n-1)
vì 10 chia hết cho 10 nên 10(3n-2n-1) chia hết cho 10
=> 3n+2 - 2n+2 +3n -2n chia hết cho 10
Ai làm nhanh nhất mình sẽ **** xin cảm ơn các bạn mình đang cần gấp

a)
\(\frac{3}{5}=\frac{18}{30};\frac{7}{10}=\frac{21}{30}\)
Gọi tử số của một phân số thỏa mãn là a
\(\Rightarrow\frac{18}{30}< \frac{a}{30}< \frac{21}{30}\Rightarrow a\in\left\{19,20\right\}\)
Vậy, tổng là : \(\frac{19+20}{30}=\frac{39}{30}\)
b)
\(\frac{1}{6}=\frac{2}{12}\)
Gọi mẫu của một phân số thỏa mãn là b
\(\Rightarrow\frac{2}{12}< \frac{2}{b}< \frac{2}{9}\Rightarrow b\in\left\{11;10\right\}\)
Vậy, tổng là : \(\frac{2}{11}+\frac{2}{10}=\frac{20+22}{110}=\frac{42}{110}=\frac{21}{55}\)

b) = \(\frac{3}{4}\div\)\(\left(-\frac{1}{3}+\frac{2}{3}+\frac{1}{2}\right)\)
= \(\frac{3}{4}\div\frac{5}{6}\)
= \(\frac{9}{10}\)
c) \(\frac{16.2^3}{4}\)
\(=4.8=32\)
\(a)\left|-\frac{1}{2}\right|+3^0+\frac{1}{4}+4+2021^0.\)
\(=\frac{1}{2}+1+\frac{1}{4}+4+1\)
\(=\left(\frac{1}{2}+\frac{1}{4}\right)+\left(1+4+1\right)\)
\(=\frac{3}{4}+6=\frac{27}{4}\)
\(b)\frac{3}{4}\div\left(-\frac{1}{3}\right)+\frac{3}{4}\div\frac{2}{3}+\frac{3}{4}\div\frac{1}{2}\)
\(=\frac{3}{4}\div\left(-\frac{1}{3}+\frac{2}{3}+\frac{1}{2}\right)\)
\(=\frac{3}{4}\div\frac{5}{6}=\frac{9}{10}\)

a, ( x - 3 ) . ( x - 4 ) = 0
=> x - 3 = 0 hoặc x - 4 = 0
Nếu x - 3 = 0 => x = 3
Nếu x - 4 = 0 => x = 4
b, (\(\frac{1}{2}\)x - 4 ) . ( x - \(\frac{1}{4}\)) = 0
=>( \(\frac{1}{2}\)x - 4 ) = 0 Hoặc ( x - \(\frac{1}{4}\)) = 0
Nếu ( \(\frac{1}{2}\)x - 4 ) = 0 => x = \(\frac{8}{1}\)
Nếu ( x - \(\frac{1}{4}\)) = 0 => x = \(\frac{1}{4}\)
c, (\(\frac{1}{3}\)- x ) . ( \(\frac{1}{2}\)+ 1 : x ) = 0
=> ( \(\frac{1}{3}\)- x ) = 0 Hoặc ( \(\frac{1}{2}\)+ 1 : x ) = 0
Nếu (\(\frac{1}{3}\)- x ) = 0 => x = \(\frac{1}{3}\)
Nếu ( \(\frac{1}{2}\)+ 1 : x ) = 0 => x = \(\frac{-2}{1}\)
d, ( x + 3 ) . ( x - 4 ) + 2.(x + 3 ) = 0
=> (X + 3 ) = 0 Hoặc ( x - 4 ) = 0 Hoặc 2. ( x + 3 ) = 0
Nếu x + 3 = 0 => x = 0
Nếu ( x - 4 ) = 0 => x = 4
Nếu 2.(x + 3) = 0 => x = 3
# Cụ MAIZ
a. ( x - 3 ) ( x - 4 ) = 0
<=> \(\orbr{\begin{cases}x-3=0\\x-4=0\end{cases}}\)
<=> \(\orbr{\begin{cases}x=3\\x=4\end{cases}}\)
b. \(\left(\frac{1}{2}x-4\right)\left(x-\frac{1}{4}\right)=0\)
<=> \(\orbr{\begin{cases}\frac{1}{2}x-4=0\\x-\frac{1}{4}=0\end{cases}}\)
<=> \(\orbr{\begin{cases}x=8\\x=\frac{1}{4}\end{cases}}\)

Bài làm :
\(a\text{)}...\Leftrightarrow\orbr{\begin{cases}x-3=0\\x-4=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=3\\x=4\end{cases}}\)
\(b\text{)}...\Leftrightarrow\orbr{\begin{cases}\frac{1}{2}x-4=0\\x-\frac{1}{4}=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}\frac{1}{2}x=4\\x=0+\frac{1}{4}\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=8\\x=\frac{1}{4}\end{cases}}\)
\(c\text{)}...\Leftrightarrow\orbr{\begin{cases}\frac{1}{3}-x=0\\\frac{1}{2}+1\div x=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=\frac{1}{3}-0\\1\div x=-\frac{1}{2}\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=\frac{1}{3}\\x=-2\end{cases}}\)
\(d\text{)}...\Leftrightarrow\left(x+3\right)\left(x-4+2\right)=0\Leftrightarrow\left(x+3\right)\left(x-2\right)=0\Leftrightarrow\orbr{\begin{cases}x+3=0\\x-2=0\end{cases}\Leftrightarrow}\orbr{\begin{cases}x=-3\\x=2\end{cases}}\)

Bài làm :
\(a,\left(x-3\right)\left(x-4\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x-3=0\\x-4=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=3\\x=4\end{cases}}\)
\(b,\left(\frac{1}{2}x-4\right)\left(x-\frac{1}{4}\right)=0\)
\(\Rightarrow\orbr{\begin{cases}\frac{1}{2}x-4=0\\x-\frac{1}{4}=0\end{cases}}\Rightarrow\orbr{\begin{cases}\frac{1}{2}x=4\\x=\frac{1}{4}\end{cases}}\Rightarrow\orbr{\begin{cases}x=8\\x=\frac{1}{4}\end{cases}}\)
\(c,\left(\frac{1}{3}-x\right).\left(\frac{1}{2}+1:x\right)=0\)
\(\Rightarrow\orbr{\begin{cases}\frac{1}{3}-x=0\\\frac{1}{2}+1:x=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=\frac{1}{3}\\x=-2\end{cases}}\)
\(d,\left(x+3\right)\left(x-4\right)+2\left(x+3\right)=0\)
\(\Rightarrow\left(x+3\right)\left(x-4+2\right)=0\)
\(\Rightarrow\left(x+3\right)\left(x-2\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x+3=0\\x-2=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=-3\\x=2\end{cases}}\)
Học tốt nhé

Bài làm :
\(a\text{)}...\Leftrightarrow\orbr{\begin{cases}x-3=0\\x-4=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=3\\x=4\end{cases}}\)
\(b\text{)}...\Leftrightarrow\orbr{\begin{cases}\frac{1}{2}x-4=0\\x-\frac{1}{4}=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}\frac{1}{2}x=4\\x=0+\frac{1}{4}\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=8\\x=\frac{1}{4}\end{cases}}\)
\(c\text{)}...\Leftrightarrow\orbr{\begin{cases}\frac{1}{3}-x=0\\\frac{1}{2}+1\div x=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=\frac{1}{3}-0\\1\div x=-\frac{1}{2}\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=\frac{1}{3}\\x=-2\end{cases}}\)
\(d\text{)}...\Leftrightarrow\left(x+3\right)\left(x-4+2\right)=0\Leftrightarrow\left(x+3\right)\left(x-2\right)=0\Leftrightarrow\orbr{\begin{cases}x+3=0\\x-2=0\end{cases}\Leftrightarrow}\orbr{\begin{cases}x=-3\\x=2\end{cases}}\)

a) Thay \(x=1\)vào đa thức P ta được:
\(P=3.1^3+4.1^2-8.1+1=3+4-8+1=0\)
Vậy \(x=1\)là nghiệm của đa thức
b) \(P=3x^3+4x^2-8x+1=\left(3x^3+3x^2-9x\right)+\left(x^2+x-3\right)+4\)
\(=3x\left(x^2+x-3\right)+\left(x^2+x-3\right)+4=\left(x^2+x-3\right)\left(3x+1\right)+4\)
Thay \(x^2+x-3=0\)vào đa thức P ta được : \(P=4\)