Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

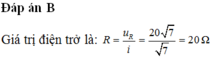
Mạch chỉ chứa R và C nên điện áp hai đầu R và C vuông pha với nhau. Suy ra:
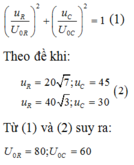
Do đó điện áp hiệu dụng hai đầu điện trở là:
![]()
Giá trị của điện dung C là:
![]()

\(2LC\omega^2=1\rightarrow2Z_L=Z_C\rightarrow2u_L=-uc\)
\(u_m=u_R+u_L+u_c=40+\left(-30\right)+60=70V\)
Chọn B

Đáp án C.
lúc đầu ta có :
UMB=2UR => ZMB=2R <=> ZC=\(\sqrt{3}\)R mà C=\(\frac{L}{R^2}\) => ZL=\(\frac{R}{\sqrt{3}}\)
lúc sau ta có Uc' max :
Zc'.ZL=R2+ \(Z^2_L\) => Zc'=\(\frac{4R}{\sqrt{3}}\)
\(\text{tanφ}=\frac{Z_L-Z_C}{R}\Rightarrow\tan\varphi=-\sqrt{3}\Rightarrow\varphi=-\frac{\pi}{3}\)

Đáp án C
+ Điện trở của mạch R = u R i = 20 Ω
Điện áp trên điện trở và trên tụ điện luôn vuông nhau tại cùng một thời điểm bất kì, ta có:

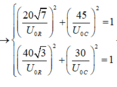
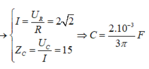

Có: \(L=CR^2=Cr^2\Rightarrow R^2=r^2=Z_LZ_C,URC=\sqrt{3U}_{Lr}\Leftrightarrow Z^2_{RC}=3Z^2_{Lr}\Leftrightarrow R^2+Z^2_C=3\left(Z^2_L+R^2\right)\)
\(\Leftrightarrow-3Z^2_L+Z^2_C=2R^2\) (*) \(R^2=Z_LZ_C\) (**)
Từ (*) và (**) có: \(Z_L=\frac{R}{\sqrt{3}};Z_C=\sqrt{3}R\Rightarrow Z=\sqrt{\left(R+r\right)^2Z^2_{LC}}=\frac{4R}{\sqrt{3}}\Rightarrow\cos\phi=\frac{R+r}{Z}=\frac{\sqrt{3}}{2}\approx0,866\)
A đúng

Ta có Um không đổi và để UAm luôn không đổ vs mọi gtri của R thì : Um=UAm hay ZL=2ZC =2.100=200 → L=2/π ( D)
Sử dụng hình vẽ suy luận cho nhanh : R ZL ZC UAm Um
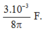
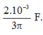
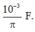
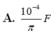
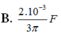
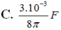
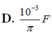
Giải thích: Đáp án C
+ Điện áp trên tụ và trên điện trở luôn vuông pha nên:
+ Xét đoạn mạch chỉ có điện trở R: Khi điện áp tức thời trên R có giá trị 20 7 thì cường độ dòng điện tức thời có giá trị 7 A.
Đối với đoạn mạch chỉ có R, ta có: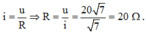
Cường độ dòng điện dực đại trong mạch: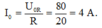
+ Xét đoạn mạch chỉ có tụ điện: