Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án B
? Lời giải:
+ Do V, T không đổi nên ta có:
v 3 = p 3 p 2 . v 1 = 0 , 8 mol
khí thoát ra 0,2 mol.

Đáp án: C
Ban đầu, khí Nito có khối lượng mm, thể tích V, áp suất p, nhiệt độ T
PT: p 1 V = m M R T 1
- Sau một thời gian, khí Heli có khối lượng m′, thể tích V, áp suất p2, nhiệt độ T
PT: p 2 V = m ' M R T 2
Lấy 2 1 ta được:
p 2 p 1 = m ' m ↔ 0,8 1 = m ' m → m ' = 0,8 m
=> Lượng khí Nito đã thoát ra:
Δ m = m − m ' = m − 0,8 m = 0,2 m = 0,2.1.28 = 5,6 g
Số mol khí Nito thoát ra ngoài là: n = m M = 5,6 28 = 0,2 m o l
Vậy lượng khí đã thoát ra ngoài bằng: 0,2mol

Chọn D.
Áp dụng phương trình Cla-pê-rôn – Men-đê-lê-ép:
+ Trạng thái 1 (khi chưa tăng nhiệt độ):
Khối lượng m1, p1 = 5.105 Pa, V1 = 4,8 lít, T1 = 287 K
Từ phương trình:
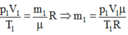
+ Trạng thái 2 (khi đã tăng nhiệt độ):
Khối lượng m2, p2 = p1 = 5.105 Pa, V2 = V1 = 4,8 lít, T2 = 26 + 273 = 287 K.
Từ phương trình:
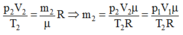
Khối lượng khí thoát ra ngoài:
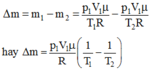
Thay số:
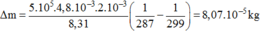

Gọi m i , rrn là khối lượng khí trong bình trước và sau khi nung nóng bình.
Áp dụng phương trình Menđêlêep - Clapêrôn ta có:
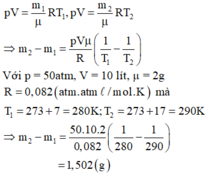

Xét lượng khí còn lại trong bình
Trạng thái 1: V 1 = V/2; T 1 = 27 + 273 = 300 K; p 1 = 40 atm.
Trạng thái 2: V 2 = V; T 2 = 12 + 273 = 285 K; p 2 = ? atm,
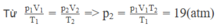

Đáp án D.
Ta có: p 1 T 1 = p 2 T 2 ⇒ T 2 = p 2 p 1 . T 1 = 1500 K = 1227 0 C

Từ phương trình: \(p_V=nRT\)
Suy ra:
\(V=\frac{nRT}{p}=\frac{3\times8.31\times300}{600000}=0.012\left(m^3\right)=12\left(l\right)\)

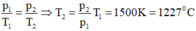
Đáp án B.
Do V,T không đổi nên ta có: