RM
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HQ
Hà Quang Minh
Giáo viên
2 tháng 10 2023
Hai số nguyên đối nhau thì thỏa mãn đề bài, ví dụ: 2\( \vdots \)(-2)và (-2)\( \vdots \)2
JK
1 tháng 8 2019
\(a,n+6⋮n\)
\(\Rightarrow6⋮n\)
\(\Rightarrow n\inƯ\left(6\right)\)
\(\Rightarrow n\in\left\{-1;1;-2;2;-3;3;-6;6\right\}\)
\(b,n+9⋮n+1\)
\(\Rightarrow n+1+8⋮n+1\)
\(\Rightarrow8⋮n+1\)
\(\Rightarrow n+1\inƯ\left(8\right)\)
\(\Rightarrow n+1\in\left\{-1;1;-2;2;-4;4;-8;8\right\}\)
\(\Rightarrow n\in\left\{-2;0;-3;1;-5;3;-9;7\right\}\)
\(c,n-5⋮n+1\)
\(\Rightarrow n+1-6⋮n+1\)
\(\Rightarrow6⋮n+1\)
\(\Rightarrow n+1\inƯ\left(6\right)\)
\(\Rightarrow n+1\in\left\{-1;1;-2;2;-3;3;-6;6\right\}\)
\(\Rightarrow n\in\left\{-2;0;-3;0;-4;2;-7;5\right\}\)
\(d,2n+7⋮n-2\)
\(\Rightarrow2n-4+11⋮n-2\)
\(\Rightarrow2\left(n-2\right)+11⋮n-2\)
\(\Rightarrow11⋮n-2\)
\(\Rightarrow n-2\inƯ\left(11\right)\)
\(\Rightarrow n-2\in\left\{-1;1;-11;11\right\}\)
\(\Rightarrow n\in\left\{1;3;-9;13\right\}\)
SG
6
16 tháng 4 2017
Có nhiều cặp 2 số nguyên a, b khác nhau mà \(a⋮b\) và\(b⋮a\) <=> a và b là hai số nguyên đối nhau.
Ví dụ : 2\(⋮\)(-2) ; (-2)\(⋮\)2
25 tháng 1 2016
n+2 chia hết n-3 \(\left(n\ne3;n\in Z\right)\)
Mà n-3 chia hết n-3
=> [(n+2)-(n-3)] chia hết n-3
<=> [n+2-n+3] chia hết n-3
=> 5 chia hết n-3
=> n-3 thuộc {-1 ; -5 ; 5; 1 }
Ta có bảng
| n-3 | -1 | -5 | 1 | 5 |
| n | 2 | -2 | 4 | 8 |
Thử lại : đúng
Vậy \(n\in\left\{2;-2;4;8\right\}\)
BB
0
VP
5
17 tháng 1 2018
2 chia hết cho 4 ; 4 chia hết cho 2
6 chia hết cho 3 ; 3 chia hết cho 6
17 tháng 1 2018
Những số nguyên a, b khác nhau mà a chia hết cho b và b chia hết cho a là những số đối nhau.
Không tin bạn cứ thử.
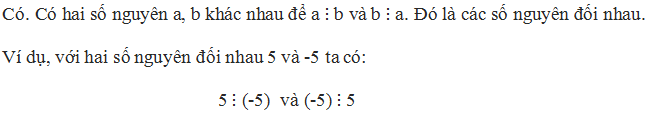
có , vd: -1 chia hết cho 1 ; 1 chia hết cho -1
tóm lại , đó là 2 số nguyên đối nhau
có đó: ví dụ 1 và -1; 2 và -2; 3 và -3....
tick nha