Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 7: Phương án làm giảm hao phí hữu hiệu nhất là:
A. Tăng tiết diện dây dẫn B. Chọn dây dẫn có điện trở suất nhỏ
C. Tăng hiệu điện thế D. Giảm tiết diện dây dẫn
vì: Phương án làm giảm hao phí hữu hiệu nhất là tăng hiệu điện thế

\(R=\frac{\rho l}{s};I=\frac{U}{R}\)
R tỷ lệ thuận với điện trở suất và chiều dài; tỷ lệ nghịch với tiết diện
I tỷ lệ nghịch với R
Từ đó suy ra bạn sẽ tìm được câu đúng sai

\(0,5mm^2=0,5.10^{-6}m^2=5.10^{-7}m^2\)
\(3mm^2=3.10^{-6}m^2\)
Điện trở dây có tiết diện \(0,5mm^2\) là \(R=\rho\frac{l}{s}=\rho\frac{l}{5.10^{-7}}=\frac{U}{R}=\frac{6}{1,5}=4\Omega\Rightarrow\rho l=4.5.10^{-7}=2.10^{-6}\)
Điện trở dây có tiết diện \(3mm^2\) là \(R=\rho\frac{l}{3.10^{-6}}=\frac{2.10^{-6}}{3.10^{-6}}=\frac{2}{3}\Omega\)
Cường độ dòng điện khi đó là
\(I=\frac{U}{R}=6.\frac{3}{2}=9A\)

Chọn B. Giảm 2 lần
Điện trở của đường dây tải điện được tính bằng công thức: 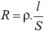
Công suất hao phí do tỏa nhiệt trên đường dây tải điện là: 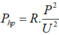
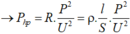
Như vậy ta thấy rằng P h p tỷ lệ nghịch với tiết diện S của đường dây tải. Do đó nếu đường dây tải có tiết diện tăng gấp đôi thì công suất hao phí thì tỏa nhiệt sẽ giảm 2 lần.

Ta có công thức tính công suất hao phí là Php=(R.P2)/U2 .
Theo công thức thì Php tỉ lệ thuận với điện trở R mà R thì tỉ lệ nghịch với tiết diện S của dây theo công thức R=(ρ.l)/S.
Do vậy khi tiết diện dây dẫn S tăng 2 lần thì công suất hao phí giảm 2 lần.
vaayj chonj B

Chọn B. Tăng lên bốn lần.
Điện trở của đường dây tải điện được tính bằng công thức: 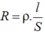
Ta có công thức tính tiết diện dây dẫn tròn là: S = π d 2 /4
(d: là đường kính của tiết diện dây dẫn).
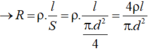
Công suất hao phí do tỏa nhiệt trên đường dây tải điện là: 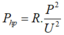
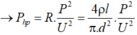
Như vậy ta thấy rằng nếu U, P và l không thay đổi thì P h p tỷ lệ nghịch với bình phương đường kính tiết diện dây tải.
Nếu dùng dây dẫn có đường kính tiết diện giảm đi 1 nửa thì công suất hao phí vì tỏa nhiệt tăng 4 lần.

Ta có: \(P_{hp}=\dfrac{P^2\cdot R}{U^2}\)
Mà \(R=\dfrac{l}{S}\cdot\rho\)
Từ hai công thức trên ta suy ra: \(P_{hp}=\dfrac{P^2\cdot R\cdot\rho}{U^2\cdot S}\)
Nhìn vào công thức nếu giảm \(S\) 2 lần và tăng \(U\) 2 lần thì \(P_{hp}\) giảm 2 lần do \(P_{hp}\) tỉ lệ nghịch với \(U^2,S\)
C
C