Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tứ giác AMBC có
K là trung điểm của AB
K là trung điểm của MC
Do đó: AMBC là hình bình hành
Suy ra: AM//BC và AM=BC(1)
Xét tứ giác ABCN có
E là trung điểm của AC
E là trung điểm của BN
Do đó: ABCN là hình bình hành
Suy ra: AN//BC và AN=BC(2)
Từ (1) và (2) suy ra A là trung điểm của MN

Bạn tự vẽ hình nha
Xét tam giác AKM và tam giác BKC có:
AK = BK (K là trung điểm của AB)
AKM = BKC ( 2 góc đối đỉnh)
KM = KC (gt)
⇒ Tam giác AKM = Tam giác BKC (c.g.c)
⇒ AM = BC (2 cạnh tương ứng) (1)
AMK = BCK (2 góc tương ứng) mà 2 góc này ở vị trí so le trong
⇒ AM // BC (2)
Xét tam giác AEN và tam giác CEB có:
AE = CE (E là trung điểm của AC)
AEN = CEB (2 góc đối đỉnh)
EN = EB (gt)
⇒ Tam giác AEN = Tam giác CEB (c.g.c)
⇒AN = CB (2 cạnh tương ứng) (3)
ANE = CBE (2 góc tương ứng) mà 2 góc này ở vị trí so le trong
⇒ AN // CB (4)
Từ (1) và (3)
⇒ AM = AN (5)
Từ (2) và (4)
⇒ A, M, N thẳng hàng (6)
Từ (5) và (6)
⇒ A là trung điểm của MN
Vote me~~

Trả lời:
Mình ghi các bước giải nha!!
B1: Xét \(\Delta MAK\)và \(\Delta CBK\)
\(\Rightarrow MA=BC\)( 2 cạnh tương ứng )
Mà \(AMKvàKCB\left(SLT\right)\)
\(\Rightarrow AM//BC\)
B2: Xét \(\Delta NAE\)và \(\Delta BCE\)
\(\Rightarrow AN=BC\) ( 2 cạnh tương ứng )
Mà.........( tương tự như phần trên)
B3: Do \(AM//BC\) và \(AN//BC\) \(\left(CMT\right)\)
\(\Rightarrow M;A;N\) thẳng hàng
mà \(AM=BC;AN=BC\)
\(\Rightarrow\) \(AM=AN\)
Hay A là trung điểm của \(MN\)
~ học tốt ~

C/m tam giác NEA và tam giác BEC có :
AE=EC(gt) NE=EB(gt) NEA = BEC ( hai góc đối đỉnh )
=> tam giác NEA = tam giác BEC ( c.g.c)
=> ANE = CBE ( hai góc tương ứng) => NA // CB (1)
=> NA = CB ( 2 cạnh tương ứng )(3)
Tương tự cm tam giác MKA = tam giác CKB ( c.g.c) => AMK= BCK => AM // CB(2)
=> AM = CB(4)
Từ (1) (2) => N, A, M thẳng hàng (5)
Từ (3) (4) => AN=AM (6)
Từ (5) (6) => A là trung điểm của NM

Mình giả bài này rồi nhé, định bào bạn vào TK mình lục nhưng thôi tại mình cung đang rảnh:vv
+Xét \(\Delta AEN\) và \(\Delta CEB:\)
AE=CE(gt)
EN=EB(gt)
\(\widehat{AEN}=\widehat{CEB}\) (2 góc đối đỉnh)
=> \(\Delta AEN=\Delta CEB\left(c-g-c\right)\)
=> AN=CB(2 cạnh t/ứ)(1)
+Xét \(\Delta AKN\) và \(\Delta BKC:\)
AK=BK(gt)
MK=CK(gt)
\(\widehat{AKM}=\widehat{BKC}\) (2 góc đối đỉnh)
=> \(\Delta AKM=\Delta BKC\left(c-g-c\right)\)
=> AM=BC(2 cạnh t/ứ)(2)
Từ (1) và (2) suy ra: AM=AN (3)
Ta có: \(\left\{{}\begin{matrix}\widehat{MAK}=\widehat{CBK}\left(\Delta MAK=\Delta CKB\right)\\\widehat{NAE}=\widehat{BCE}\left(\Delta NAE=\Delta BCE\right)\end{matrix}\right.\)
Mà: \(\widehat{CBK}+\widehat{BAC}+\widehat{BCE}=180^o\)
\(\widehat{MAK}+\widehat{BAC}+\widehat{NAE}=180^o\)
=> M, A, N thẳng hàng (4)
Từ (3) và (4) suy ra: A là trung điểm của MN

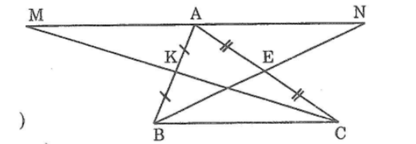
Xét ΔAKM và ΔBKC ta có:
AK = BK (Vì K là trung điểm AB)
∠(AKM) =∠(BKC) (đối đỉnh)
KM=KC (giả thiết)
Suy ra: ΔAKM = ΔBKC(c.g.c)
⇒AM =BC (hai cạnh tương ứng)
Và ∠(AMK) =∠(BCK) (2 góc tương ứng)
Suy ra: AM // BC ( vì có cặp góc so le trong bằng nhau)
Tương tự: ΔAEN= ΔCEB(c.g.c)
⇒ AN = BC (2 cạnh tương ứng)
Và ∠(EAN) =∠(ECB) (2 góc tương ứng)
Suy ra: AN // BC (vì có cặp góc so le trong bằng nhau)
Ta có: AM // BC và AN // BC nên hai đường thẳng AM và AN trùng nhau hay A,M,N thẳng hàng (1)
Lại có: AM = AN ( vì cùng bằng BC) (2)
Từ (1) và (2) suy ra: A là trung điểm của MN

A B C K M N E