Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có :3x=2y;7y=5z và x+z-y=32
=>3x=2y;7y=5z=>x/2=y/3;y/5=z/7=>x/2=5y/15;3y/15=z/7=>x/10=y/15=z/21
Áp dụng tính chất dãy tỉ số bằng nhau :
x/10=y/15=z/21=x+z-y/10+15-21=32/4=8
Suy ra :x/10=8=>x=8.10=80
y/15=8=>y=15.8=120
z/21=8=>z=8.21=168
Ta có : \(3x=2y\Rightarrow\frac{x}{2}=\frac{y}{3}\Rightarrow\frac{x}{10}=\frac{y}{15}\left(1\right)\)
\(7y=5z\Rightarrow\frac{y}{5}=\frac{z}{7}\Rightarrow\frac{y}{15}=\frac{z}{21}\left(2\right)\)
Từ ( 1 ) và ( 2 ) \(\Rightarrow\frac{x}{10}=\frac{y}{15}=\frac{z}{21}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có :
\(\frac{x}{10}=\frac{y}{15}=\frac{z}{21}=\frac{x+z-y}{10+21-15}=\frac{32}{16}=2\)
\(\Rightarrow x=10\cdot2=20\)
\(y=15\cdot2=30\)
\(z=2\cdot21=42\)

xy+3x-7y=21
<=> x(y+3) -7y = 21
<=> x(y+3) = 21+7y
<=> x(y+3) = 7(y+3)
<=> (x-7)(y+3)=0
Suy ra nghiệm của ptr là
x=7, y tùy ý thuộc Z
x tùy ý thuộc Z, y=-3.

Chọn C.
Phương pháp: Đưa bài toán về tìm m để hệ có nghiệm duy nhất.
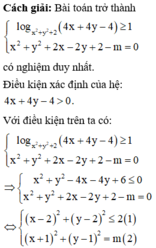


 bit lm bài này k giup tui
bit lm bài này k giup tui

Xét tổng (x-2y)+(4y-5z)+(z-3x)=-2x+2y-4z là sỗ chẵn với mọi dấu giá trị tuyệt đối .Mà 2011 lẻ.Suy ra vô nghiệm