Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác DEBF có
BE//DF
BE=DF
Do đó: DEBF là hình bình hành
b: ta có: DEBF là hình bình hành
nên Hai đường chéo DB và EF cắt nhau tại trung điểm của mỗi đường(1)
Ta có:ABCD là hình bình hành
nên hai đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường(2)
Từ (1) và (2) suy ra BD,EF,AC đồng quy

a) bạn tự vẽ hình nhé!
Có : \(AE=BE=\frac{1}{2}AB\) (đề cho)
\(DF=CF=\frac{1}{2}DC\) (đề cho)
mà \(AB=CD\)
\(\Rightarrow\) \(AE=BE=DF=CF\)
Xét tứ giác AEFD có:
\(AE=DF\) (cmt) và AE//DF( AB//CD)
\(\Rightarrow\) Tứ giác AEFD là hình bình hành
Xét tứ giác AECF có :
AE = CF ( cmt) và AE//CF ( AB//CD)
\(\Rightarrow\) Tứ giác AECF là hình bình hành
M là giao điểm của AF và DE
\(\Rightarrow\) AM = FM=\(\frac{1}{2}AF\) ( tính chất đ/chéo hbhành) (1)
N là giao điểm của BF và CE
\(\Rightarrow\) EN = CN=\(\frac{1}{2}CE\) ( tính chất đ/chéo hbhành) (2)
Có AF = AM + FM
CE = EN + CN
mà AE = CE ( AECF là hbh)
Từ (1) và (2) suy ra MF= EN và MF//EN ( AF//CE )
\(\Rightarrow\) EMFN là hình bình hành (3)
Có AE = AD ( cùng bằng 2AB ) và AEFD là hình bình hành nên AEFD là hình thoi
\(\Rightarrow\) AF \(\perp\) DE tại M hay góc EMF = 90 độ (4)
Từ (3) và (4) suy ra : EMFN là hcn

A D F M E B C N
a) Tứ giác AEFD là hình thoi, tứ giác AECF là hình bình hành (tự chứng minh).
b) Tứ giác AECF là hình bình hành nên EN // FM. Tứ giác AECF là hình bình hành nên EM // FN. AEFD là hình thoi nên AF \(\perp\) DE.
Hình bình hành EMFN có \(\widehat{M}=90^o\) nên là hình chữ nhật.
c) Hình chữ nhật EMFN là hình vuông
\(\Leftrightarrow\) ME = MF \(\Leftrightarrow\) DE = AF (vì DE = 2ME, AF = 2MF)
\(\Leftrightarrow\) Hình thoi AEFD có hai đường chéo bằng nhau
\(\Leftrightarrow\) AEFD là hình vuông \(\Leftrightarrow\) \(\widehat{A}=90^o\).
\(\Leftrightarrow\) Hình bình hành ABCD là hình chữ nhật.
Như vậy, hình chữ nhật EMFN là hình vuông nếu ABCD là hình chữ nhật.

a) Ta có: AB//CD(gt)
mà E∈AB và F∈CD
nên AE//DF và EB//FC
Xét tứ giác AEFD có AE//DF(cmt)
nên AEFD là hình thang có hai đáy là AE và DF(Định nghĩa hình thang)
Hình thang AEFD(AE//DF) có
O là trung điểm của EF(gt)
OM//AE//DF(MN//AB//DC, E∈AB, O∈MN, F∈DC)
Do đó: M là trung điểm của AD(Định lí 3 về đường trung bình của hình thang)
Xét tứ giác BEFC có BE//FC(cmt)
nên BEFC là hình thang có hai đáy là BE và FC(Định nghĩa hình thang)
Hình thang BEFC(BE//FC) có
O là trung điểm của EF(gt)
ON//EB//FC(MN//AB//DC, E∈AB, O∈MN, F∈CD)
Do đó: N là trung điểm của BC(Định lí 3 về đường trung bình của hình thang)
Xét ΔABD có
M là trung điểm của AD(cmt)
E là trung điểm của AB(gt)
Do đó: ME là đường trung bình của ΔABD(Định nghĩa đường trung bình của tam giác)
⇒ME//BD và ME=BD2ME=BD2(Định lí 2 về đường trung bình của tam giác)(1)
Xét ΔBDC có
N là trung điểm của BC(cmt)
F là trung điểm của CD(gt)
Do đó: NF là đường trung bình của ΔBDC(Định nghĩa đường trung bình của tam giác)
⇒NF//BD và NF=BD2NF=BD2(Định lí 2 về đường trung bình của tam giác)(2)
Từ (1) và (2) suy ra ME//NF và ME=NF
Xét tứ giác EMFN có ME//NF(cmt) và ME=NF(cmt)
nên EMFN là hình bình hành(Dấu hiệu nhận biết hình bình hành)
b) Xét ΔBAC có
E là trung điểm của AB(gt)
N là trung điểm của BC(cmt)
Do đó: EN là đường trung bình của ΔBAC(Định nghĩa đường trung bình của tam giác)
⇒EN//AC và EN=AC2EN=AC2(Định lí 2 về đường trung bình của tam giác)
Hình bình hành EMFN trở thành hình thoi khi EM=EN
mà EM=BD2EM=BD2(cmt) và EN=AC2EN=AC2(cmt)
nên BD=AC
Vậy: Khi hình thang ABCD có thêm điều kiện BD=AC thì EMFN là hình thoi

Bài 1:
a: Xét tứ giác ABEF có
BE//AF
BE=AF
BE=BA
Do đó: ABEF là hình thoi
b: Xét ΔBIE có BI=BE
nên ΔBIE cân tại B
mà góc IBE=60 độ
nên ΔBIE đều
=>góc I=60 độ
Xét tứ giác AFEI có
EF//AI
góc I=góc A
Do đó AFEI là hình thang cân
c: Xét ΔBAD có
BF là đường trung tuyến
BF=AD/2
Do đó: ΔBAD vuông tại B
=>DB vuông góc với BI
Xét tứ giác BICD có
BI//CD
BI=CD
Do đó: BICD là hình bình hành
mà DB vuông góc với BI
nên BICD là hình chữ nhật
d: Xét ΔAED có
EF la trung tuyến
FE=DA/2
Do đó: ΔAED vuông tại E
=>góc AED=90 độ

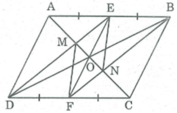
Xét ∆ EOM và ∆ FON có: ∠ (MEO) = ∠ (NFO) (so le trong do DE//BF)
OE = OF (tính chất hình bình hành)
∠ (MOE)= ∠ (NOF) (đối đỉnh )
Suy ra: ∆ EOM = ∆ FON (g.c.g) ⇒ OM = ON
Vậy tứ giác EMFN là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường).


Bài làm :
A B C D E F
a/ Xét \(\diamond EBFD\), có :
\(\Rightarrow \diamond EBFD\) là hình bình hành \(\Rightarrow DE=BF,\:EB//EF\)(1)
b/ Xét \(\diamond AECF\), có :
\(\Rightarrow\:\diamond AECF\) là hình bình hành \(\Rightarrow AF=EC, AF//EC\) (2)
Từ (1) và (2) \(\Rightarrow \diamond EMFN\) là hình bình hành.