Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) (P) là parabol đi qua gốc toạ độ O(0; 0) ; điểm (1; 1/2) và điểm (-1;1/2)
b) A \(\in\) (P) => yA = \(\frac{1}{2}\). xA2 = \(\frac{1}{2}\). (-1)2 = \(\frac{1}{2}\)=> A (-1; \(\frac{1}{2}\))
B \(\in\) (P) => yB = \(\frac{1}{2}\).xB2 = \(\frac{1}{2}\).4 = 2 => B (2; 2)
+) đường thẳng có hệ số góc bằng \(\frac{1}{2}\) có dạng y = \(\frac{1}{2}\)x + b (d)
A \(\in\) d => yA = \(\frac{1}{2}\).xA + b => \(\frac{1}{2}\) = \(\frac{1}{2}\). (-1) + b => b = 1
Vậy đường thẳng (d) có dạng y = \(\frac{1}{2}\)x + 1
Nhận xét: yB = \(\frac{1}{2}\).xB + 1 => B \(\in\) (d)

- Tập xác định : D = R
- Hàm số trên là hàm nghịch biến khi x > 0 và đồng biến khi x < 0
Bảng giá trị :
x -4 -2 0 2 4
y -8 -2 0 -2 -8


PT hoành độ giao điểm của (p) và (d) là:
x\(^2\)=x+2
=>x\(^2\)-x -2=0
Ta có: a=1,b=-1, c=-2:a-b+c=0
=>pt có 2no pb x1=-1 x 2=2
Thay x vào tìm y

Bài giải:
Vẽ đồ thị: y =  x2
x2
|
x |
-6 |
-3 |
0 |
3 |
6 |
|
y = |
12 |
3 |
0 |
3 |
12 |
y = -x + 6
- Cho x = 0 => y = 6.
- Cho y = 0 => x = 6.
Vẽ đồ thị: xem hình bên dưới.
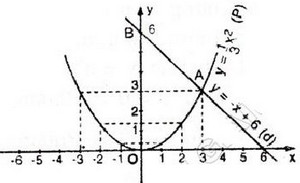
b) Giá trị gần đúng của tọa độ câc giao điểm (thực ra đây là giá trị đúng).
Hai đồ thị cắt nhau tại hai điểm A và B.
Theo đồ thị ta có A(3; 3) và B(-6; 12).

Câu 2:
a) Để đồ thị hàm số \(y=\left(m+1\right)x^2\) đi qua điểm A(1;2) thì
Thay x=1 và y=2 vào hàm số \(y=\left(m+1\right)x^2\), ta được:
m+1=2
hay m=1
Vậy: m=1

Tập xác định : R
Chiều biến thiên : hàm số đồng biến trên \(\left(-\infty;0\right)\)
hàm số nghịch biến trên \(\left(0;+\infty\right)\)
Lập bảng giá trị để vẽ đồ thị