Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Đồ thị hàm số y = 0,5x + 2 là đường thẳng đi qua các điểm (0; 2) và (-4; 0)
Đồ thị hàm số y = 5 – 2x là đường thẳng đi qua các điểm (0; 5) và (2,5; 0)
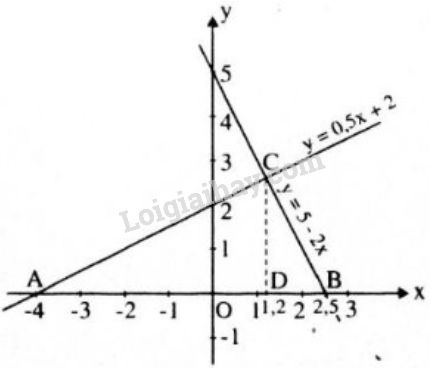
b) Ta có A(-4; 0), B(2,5; 0)
Tìm tọa độ điểm C, ta có: phương trình hoành độ giao điểm của đường thẳng y = 0,5x + 2 và y = 5 – 2x là
0,5x + 2 = 5 – 2x ⇔ 2,5x = 3
⇔ x = 1,2
Do đó y = 0,5 . 1,2 + 2 = 2,6. Vậy C (1,2; 2,6)
c) Gọi D là hình chiếu của C trên Ox ta có:
CD = 2,6; AB = AO + OB = 4 + 2,5 = 6,5 (cm)
∆ACD vuông tại D nên AC2 = CD2 + DA2
⇒AC=√2,62+5,22=√33,8≈5,81(cm)⇒AC=2,62+5,22=33,8≈5,81(cm)
Tương tự : BC=√BD2+CD2BC=BD2+CD2
=√1,32+2,62=√8,45≈2,91(cm)=1,32+2,62=8,45≈2,91(cm)
d) Ta có ∆ACD vuông tại D nên tgˆCAD=CDAD=2,65,2=12tgCAD^=CDAD=2,65,2=12
⇒ˆCAD≈26034′⇒CAD^≈26034′. Góc tạo bởi đường thẳng y=12x+2y=12x+2 và trục Ox là 26034’
Ta có ∆CBD vuông tại D nên tgˆCBD=CDBD=2,61,3=2⇒ˆCBD≈63026′tgCBD^=CDBD=2,61,3=2⇒CBD^≈63026′
Góc tạo bởi đường thẳng y = 5 – 2x và trục Ox là 1800 – 63026’ ≈ 116034’
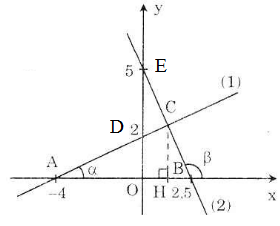
a) - Vẽ đồ thị hàm số y = 0,5x + 2 (1)
Cho x = 0 => y = 2 được D(0; 2)
Cho y = 0 => 0 = 0,5.x + 2 => x = -4 được A(-4; 0)
Nối A, D ta được đồ thị của (1).
- Vẽ đồ thị hàm số y = 5 – 2x (2)
Cho x = 0 => y = 5 được E(0; 5)
Cho y = 0 =>0 = 5 – 2x => x = 2,5 được B(2,5; 0)
Nối B, E ta được đồ thị của (2).
b) Ở câu a) ta tính được tọa độ của hai điểm A và B: A(-4; 0), B(2,5; 0)
Hoành độ giao điểm C của hai đồ thị là nghiệm phương trình:
0,5x + 2 = 5 – 2x => x = 1,2
=> y = 0,5.1,2 + 2 = 2,6
=> Tọa độ C(1,2 ; 2,6)
c) AB = AO + OB = |-4| + |2,5| = 6,5 (cm)
Gọi H là hình chiếu của C trên Ox, ta có H( 1,2; 0)
d) Gọi α là góc hợp bởi đường thẳng y = 0,5x + 2 với tia Ox.
Ta có: tgα = 0,5 => α = 26o34'
Gọi β là góc hợp bởi đường thẳng y = 5 – 2x với tia Ox (β là góc tù).
Gọi β' là góc kề bù với β, ta có:
tgβ' = -(-2) = 2 => β' = 63o26'
=> β = 180o – 63o26' = 116o34'

a, bạn tự vẽ nhé
b, Để hàm số nghịch biến khi m < 0
c, đths y = mx + 2m - 1 cắt trục tung tại điểm có tung độ bằng 3
Thay x = 0 ; y = 3 ta được : \(2m-1=3\Leftrightarrow m=2\)
d, đths y = mx + 2m - 1 cắt trục hoành tại điểm có hoành độ bằng -3
Thay x = -3 ; y = 0 ta được : \(-3m+2m-1=0\Leftrightarrow-m-1=0\Leftrightarrow m=-1\)
bổ sung hộ mình nhé
( dòng đầu tiên ) Để đths trên là hàm bậc nhất khi \(m\ne0\)

a, tự vẽ nhé
b, * Vì d3 cắt d1, hoành độ giao điểm thỏa mãn phương trình
\(-\frac{1}{3}x+3=2x-2\Leftrightarrow-\frac{7}{3}x=-5\Leftrightarrow x=\frac{15}{7}\)
Thay x = 15/7 vào d1 ta được : \(y=\frac{30}{7}-2=\frac{16}{7}\)
* Vì d3 cắt d2, hoành độ giao điểm thỏa mãn phương trình
\(-\frac{4}{3}x-2=-\frac{1}{3}x+3\Leftrightarrow-x=5\Leftrightarrow x=-5\)
Thay x = -5 vào d2 ta được : \(y=\frac{20}{3}-2=\frac{14}{3}\)
Vậy d3 cắt d1 tại A ( 15/7 ; 16/7 )
d2 cắt d1 tại B( -5 ; 14/3 )

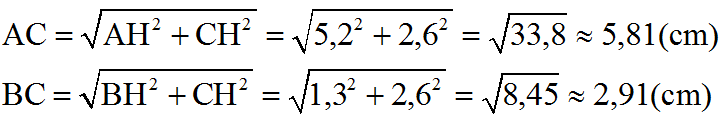
a: Thay y=0 vào (1), ta được:
2x-1=0
hay \(x=\dfrac{1}{2}\)
Thay x=0 vào (1), ta được:
\(y=2\cdot0-1=-1\)
Vậy: \(A\left(\dfrac{1}{2};0\right)\); B(0;-1)
Thay y=0 vào (2), ta được:
x-1=0
hay x=1
Thay x=0 vào (2), ta được:
y=0-1=-1
Vậy: M(1;0); N(0;-1)