Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Diện tích tiếp xúc của 4 bánh xe là
\(10.4=40\left(cm^2\right)=0,004\left(m^2\right)\)
Áp suất của ô tô là
\(p=\dfrac{F}{S}=16000:0,004=4000000\left(Pa\right)\)
ta có: diện tích 4 bánh xe tiếp xúc với mặt đất là:
10.4=40cm\(^2\)
đổi : \(40cm^2=0,004m^2\)
áp suất do ô tô tác dụng lên mặt đường là:
\(P=\dfrac{F}{S}=\dfrac{16000}{0,004}=4000000N\)/\(m^2\)
vậy............................

\(a,p=\dfrac{F}{S}=\dfrac{18000}{0,006}=3,000,000\left(Pa\right)\\ b,p=\dfrac{F}{S}=\dfrac{18,000+\left(60.10\right)}{0,006}=3,100,000\left(Pa\right)\)

a)Áp lực xe ô tô xuống mặt đường chính là trọng lực xe:
\(F=P=10m=10\cdot1500=15000N\)
b)Áp suất xe lên mặt điểm ở chỗ tiếp xúc:
\(p=\dfrac{F}{S}=\dfrac{15000}{4\cdot40\cdot10^{-4}}=937500N/m^2\)

\(\left\{{}\begin{matrix}p_1=\dfrac{F_1}{S_1}=\dfrac{P_1}{S_1}=\dfrac{360000}{1,5}=240000\left(Pa\right)\\p_2=\dfrac{F_2}{S_2}=\dfrac{P_2}{S_2}=\dfrac{15000}{250}=60\left(Pa\right)\end{matrix}\right.\)

Áp suất của ô tô là
p=\(\dfrac{F}{S}\)=\(\dfrac{20000}{0,025}\)=800000(Pa)

Tóm tắt:
\(F_1=400 000N\)
\(S_1=200dm^2=2 m^2\)
\(F_2=2000kg=20000N\)
\(S_2=0,025m^2\)
___________________
\(a, P_1=?\)
\(P_2=?\)
b, Xe nào dễ sa lầy?Vì sao?
Giải:
a,Áp suất của máy kéo lên mặt đường là:
\(P_1=\dfrac{F_1}{S_1}=\dfrac{400000}{2}=200000(Pa)\)
Áp suất của ô tô lên mặt đường là:
\(P_2=\dfrac{F_2}{S_2}=\dfrac{20000}{0,025}=800000(Pa)\)
b) Nhận xét: \(P_1 < P_2 (200000<800000) \) .Vậy nếu đi trên đất mềm, ô tô dễ bị sa lầy hơn.

a, Một chiếc xe ô tô có khối lượng 1,5 tấn, diện tích tiếp xúc của các bánh lên mặt đất là 500cm
2.Tính áp suất của xe tác dụng lên mặt đường.

2000 kg = 20000 N
Áp suất của ô tô tác dụng lên mặt đường là
\(p=\dfrac{F}{S}=20000:0,025=800000\left(Pa\right)\)
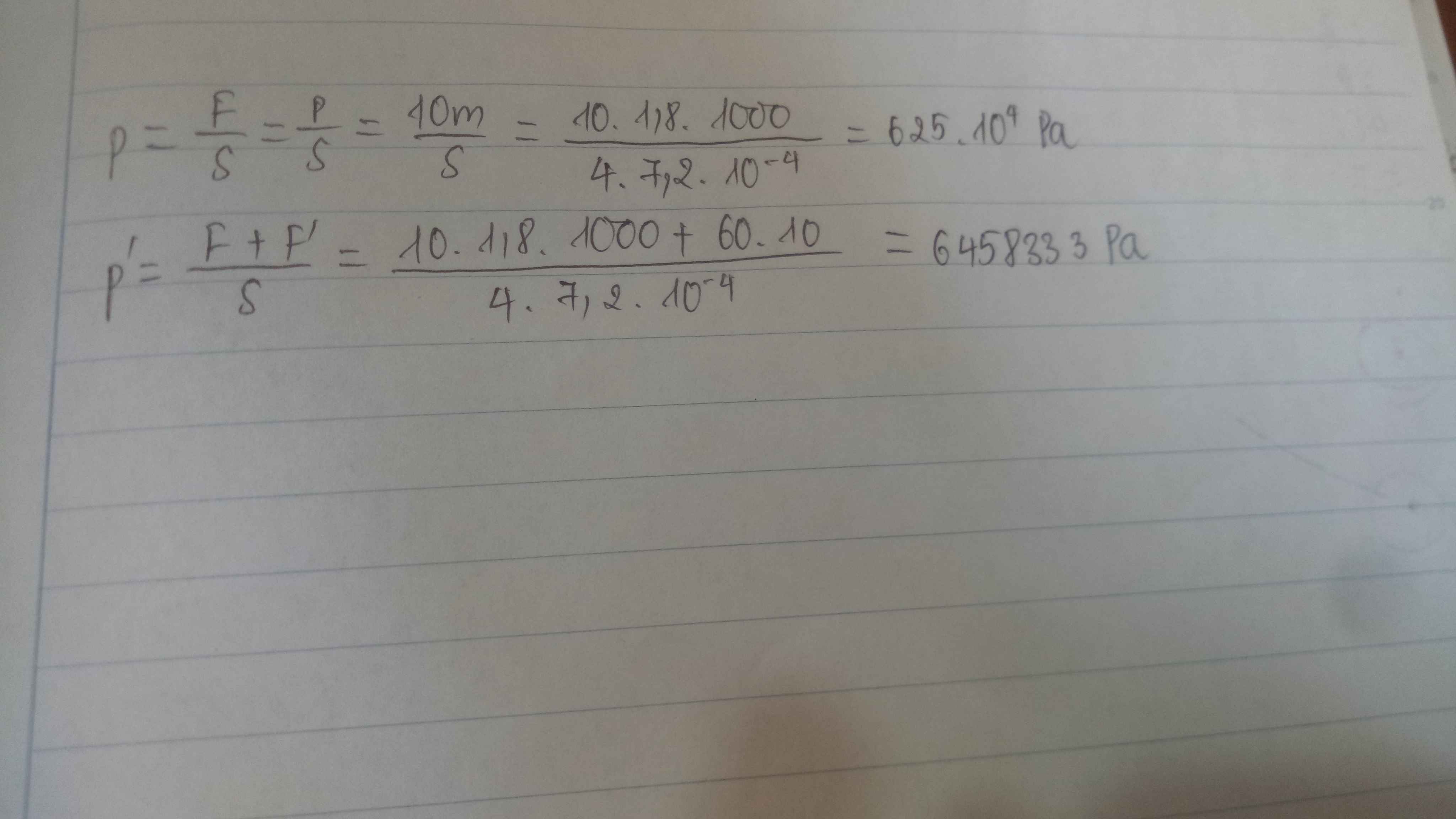
Câu 4 :
đổi 1800 kg = 18000 N
Áp suất do ô tô tác dụng lên mặt đường là
\(p=\dfrac{F}{S}=18000:0,006=3000000\left(Pa\right)\)
Đổi 0,006 m2 = 60 cm2
Trọng lực của ô tô là :
\(P=10m=10.1800=18000\left(N\right)\)
Áp xuất mà ô tô tác dụng lên mặt đường là :
\(p=\dfrac{F}{S}=\dfrac{18000}{60.10^{-4}}=120000\left(\dfrac{N}{m^2}\right)\)