Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1, Theo định lí Pytago tam giác AHB vuông tại H
\(AH=\sqrt{AB^2-BH^2}=8cm\)
2, Xét tam giác ABH và tam giác ACH có
AB = AC ; AH _ chung
Vậy tam giác ABH = tam giác ACH (ch-cgv)
3, Vì tam giác ABC cân tại A có AH là đường cao
đồng thời là phân giác
Lại có DB = CE ; AB = AC
=> AD = AE
Xét tam giác ADH và tam giác AEH có
AD = AE ( cmt ) ; AH _ chung ; ^DAH = ^EAH
Vậy tam giác ADH = tam giác AEH (c.g.c)
=> DH = HE ( 2 cạnh tương ứng )
Vậy tam giác HDE cân tại H
4, Ta có AD/AB = AE/AC => DE//BC

1: AH=8cm
2: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
Do đó: ΔABH=ΔACH
4: Xét ΔABC có AD/AB=AE/AC
nên DE//BC

a, Xét tam giác HBA vuông tại H có:
AB2=AH2+BH2(định lí py ta go)
hay 100=AH2+36
=> AH2=64
=> AH=8(cm)
b, Xét tam giác ABH và tam giác ACH có:
góc AHB=góc AHC =90 độ
AB=AC (tam giác ABC cân tại A)
AH chung
=> tam giác ABH = tam giác ACH
c,
Xét tam giác DBH và tam giác ECH có:
BD=CE (gt)
góc DBH= góc ECH (tam giác ABC Cân tại A)
BH=CH (trong tam giác cân, đường cao đồng thời là đường trung tuyến)
=> tam giác DBH=tam giác ECH
=> DH=EH( 2 cạnh tương ứng)
=> tam giác HDE cân tại H
d) Vì AB = AC; BD = CE
mà AB - BD = AD
AC - CE = AE
=> AD = AE
Vì ΔHDE cân
=> H ∈ đường trung trực cạnh DE (1)
Xét ΔADHvàΔAEHcó
AD = AE (cmt)
AH (chung)
DH = HE (cmt)
Do đó: ΔADH=ΔAEH(c−c−c)
=> AD = AE ( hai cạnh tương ứng)
=> ΔADE cân tại A
=> A ∈ đường trung trực cạnh DE (2)
(1); (2) => A,H ∈ đường trung trực cạnh DE
=>AH là đường trung trực cạnh DE
CHÚC BẠN HỌC TỐT
bn j đó ơi cảm ơn bn đx giải cho mk nhung phần b) sai rồi nha
 tham khao
tham khao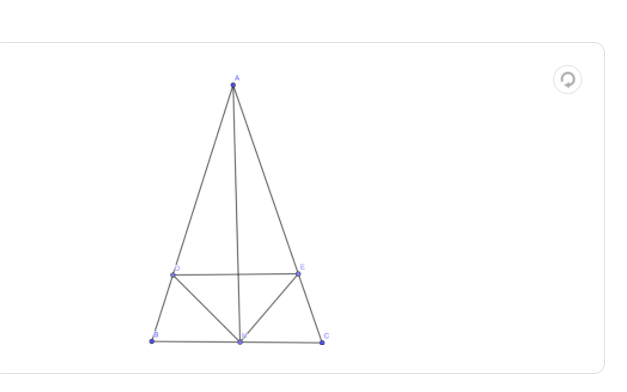
1: AH=8cm
2: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
Do đó: ΔABH=ΔACH
4: Xét ΔABC có AD/AB=AE/AC
nên DE//BC
sao lại viết tắt, ko có hình hay lời giải gì à, đọc thế ai hỉu