
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




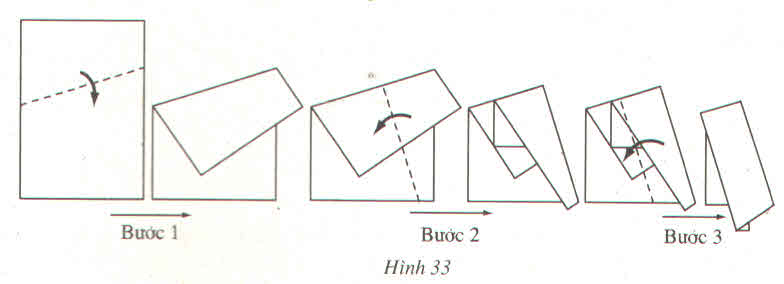
Xem hình và quan sát bước 4
Vậy các nếp gập là hình ảnh của một đường thẳng vuông góc với hai đường thẳng song song .
Xem hình và quan sát khi trải tờ giấy ra ta thấy các nếp gấp là hình ảnh của một đường thẳng vuông góc với hai đường thẳng song song.

Hướng dẫn giải:
Trước hết ta thu gọn các đơn thức đồng dạng để xác định mỗi chữ cái tương ứng với kết quả nào trong ô trống của bảng.
V 2x2 + 3x2 – 1212 x2 = 9292 x2;
Ư 5xy – 1313 xy + xy = 173173 xy;
N - 1212 x2 + x2 = 1212 x2;
U - 6x2y – 6x2y = -12x2y ;
H xy – 3xy + 5xy = 3xy;
Ê 3xy2 – (-3xy2) = 6 xy2;
Ă 7y2z3 + (-7y2z3) = 0;
L - 1515 x2 + (- 1515 x2) = - 2525 x2;

Vậy tên của tác giả cuốn Đại VIệt sử kí là Lê Văn Hưu.

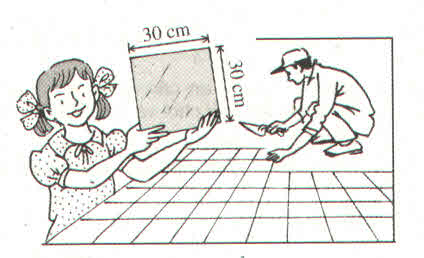
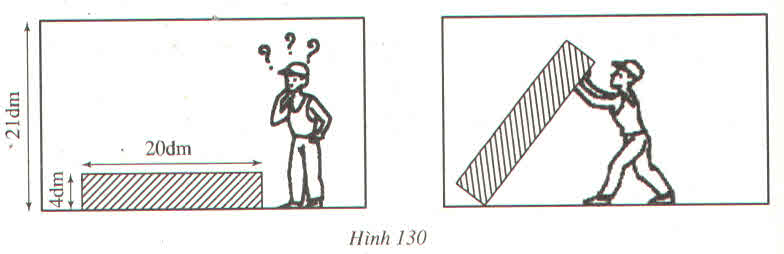
Gọi d là đường chéo của tủ. h là chiều cao của nhà. h= 21dm.
Ta có d2=202+42=400+16=416.
suy ra d= √416 (1)
Và h2=212=441, suy ra h= √441 (2)
So sánh (1) và (2) ta được d<h.
Như vậy anh Nam đẩy tủ đứng thẳng không bị vướng vào trần nhà.

Bài 1:
x y m B A C 1 1 2 1
Qua B, vẽ tia Bm sao cho Bm // Ax
Bm // Ax ( cách vẽ ) => góc A1 + góc B1 = 180o ( trong cùng phía )
Mà góc A1 = 140o ( giả thiết ) => góc B1 = 40o
Ta có: góc B1 + góc B2 = góc ABC
Mà góc ABC = 70o ( giả thiết ); góc B1 = 40o ( chứng minh trên )
=> góc B2 = 30o
Ta có: góc B2 + góc C1 = 30o + 150o = 180o
Mà hai góc này ở vị trí trong cùng phía
=> Bm // Cy ( dấu hiệu nhận biết 2 đường thẳng song song )
Ta lại có:
Ax // Bm ( cách vẽ ); Cy // Bm ( chứng minh trên )
=> Ax // Cy ( tính chất 3 quan hệ từ vuông góc đến song song ) ( đpcm )
Bài 3:
A B C F E G N M H 1 2
a) Chứng minh AH < \(\dfrac{1}{2}\) ( AB + AC )
+) Vì AH vuông góc với BC ( giả thiết )
=> AH < AB ( quan hệ giữa đường vuông góc và đường xiên ) ( 1 )
+) Vì AH vuông góc với BC ( giả thiết )
=> AH < AC ( quan hệ giữa đường vuông góc và đường xiên ) ( 2 )
+) Từ ( 1 ) và ( 2 ) => AH + AH < AB + AC
=> 2 . AH < AB + AC
=> AH < \(\dfrac{1}{2}\) ( AB + AC ) ( đpcm )
b) Chứng minh EF = BC
+) Vì BM là đường trung tuyến của tam giác ABC ( giả thiết )
=> \(\dfrac{BG}{BM}=\dfrac{2}{3}\)
=> \(\dfrac{MG}{BG}=\dfrac{1}{2}\)
=> 2 . MG = BG
Mà EM = MG ( do BM là đường trung tuyến của tam giác ABC )
=> EM + MG = BG => EG = BG
+) Vì CN là đường trung tuyến của tam giác ABC ( giả thiết )
=> \(\dfrac{CG}{CN}=\dfrac{2}{3}\)
=> \(\dfrac{GN}{CG}=\dfrac{1}{2}\)
=> 2 . GN = CG
Mà FN = GN ( do CN là đường trung tuyến của tam giác ABC )
=> FN + GN = CG => FG = CG
Góc G1 = góc G2 ( đối đỉnh )
Xét tam giác FEG và tam giác CBG có:
FG = CG ( chứng minh trên )
EG = BG ( chứng minh trên )
Góc G1 = góc G2 ( chứng minh trên )
=> tam giác FEG = tam giác CBG ( c.g.c )
=> EF = BC ( 2 cạnh tương ứng ) ( đpcm )












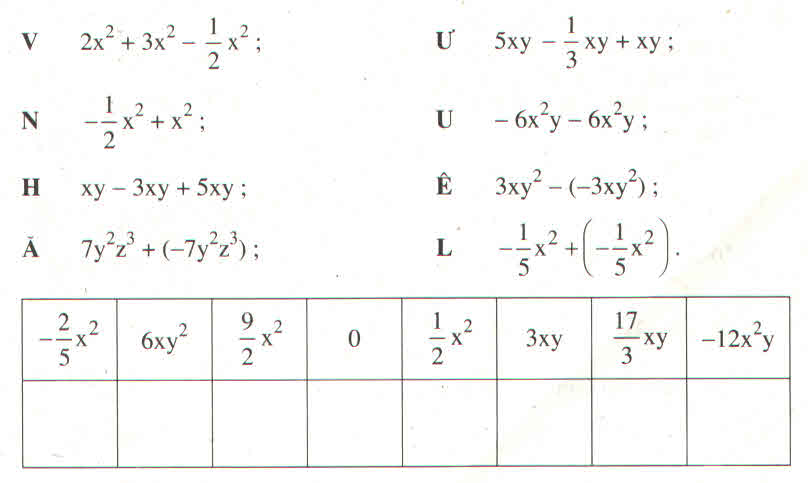




Bài 1:
Áp dụng t/c dtsbn:
a) \(\dfrac{x}{7}=\dfrac{y}{4}=\dfrac{x-y}{7-4}=\dfrac{24}{3}=8\)
\(\Rightarrow\left\{{}\begin{matrix}x=8.7=56\\y=8.4=32\end{matrix}\right.\)
b) \(\dfrac{x}{6}=\dfrac{y}{2}=\dfrac{z}{5}=\dfrac{x-y+z}{6-2+5}=\dfrac{18}{9}=2\)
\(\Rightarrow\left\{{}\begin{matrix}x=2.6=12\\y=2.2=4\\z=2.5=10\end{matrix}\right.\)
Bài 2:
Gọi số HS 3 lớp 7A,7B,7C lần lượt là a,b,c(học sinh), \(\left(a,b,c>0\right)\)
Áp dụng t/c dtsbn:
\(\dfrac{a}{5}=\dfrac{b}{6}=\dfrac{c}{7}=\dfrac{a+b+c}{5+6+7}=\dfrac{126}{18}=7\)
\(\Rightarrow\left\{{}\begin{matrix}a=7.5=35\\b=7.6=42\\c=7.7=49\end{matrix}\right.\)
Cho mình hỏi xíu dtsbn là gì ạ