Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

• Ta có: \({u_{n + 1}} = \frac{{\left( {n + 1} \right) + 1}}{{\left( {n + 1} \right) + 2}} = \frac{{n + 1 + 1}}{{n + 1 + 2}} = \frac{{n + 2}}{{n + 3}}\)
Xét hiệu:
\(\begin{array}{l}{u_{n + 1}} - {u_n} = \frac{{n + 2}}{{n + 3}} - \frac{{n + 1}}{{n + 2}} = \frac{{{{\left( {n + 2} \right)}^2} - \left( {n + 1} \right)\left( {n + 3} \right)}}{{\left( {n + 3} \right)\left( {n + 2} \right)}} = \frac{{\left( {{n^2} + 4n + 4} \right) - \left( {{n^2} + n + 3n + 3} \right)}}{{\left( {n + 2} \right)\left( {n + 1} \right)}}\\ = \frac{{{n^2} + 4n + 4 - {n^2} - n - 3n - 3}}{{\left( {n + 2} \right)\left( {n + 1} \right)}} = \frac{1}{{\left( {n + 2} \right)\left( {n + 1} \right)}} > 0,\forall n \in {\mathbb{N}^*}\end{array}\)
Vậy \({u_{n + 1}} - {u_n} > 0 \Leftrightarrow {u_{n + 1}} > {u_n}\). Vậy dãy số \(\left( {{u_n}} \right)\) là dãy số tăng.
• Ta có: \({u_n} = \frac{{n + 1}}{{n + 2}} = \frac{{\left( {n + 2} \right) - 1}}{{n + 2}} = 1 - \frac{1}{{n + 2}}\)
\(\forall n \in {\mathbb{N}^*}\) ta có:
\(n + 2 > 0 \Leftrightarrow \frac{1}{{n + 2}} > 0 \Leftrightarrow 1 - \frac{1}{{n + 2}} < 1 \Leftrightarrow {u_n} < 1\). Vậy \(\left( {{u_n}} \right)\) bị chặn trên.
\(n \ge 1 \Leftrightarrow n + 2 \ge 1 + 2 \Leftrightarrow n + 2 \ge 3 \Leftrightarrow \frac{1}{{n + 2}} \le \frac{1}{3} \Leftrightarrow 1 - \frac{1}{{n + 2}} \ge 1 - \frac{1}{3} \Leftrightarrow {u_n} \ge \frac{2}{3}\)
Vậy \(\left( {{u_n}} \right)\) bị chặn dưới.
Ta thấy dãy số \(\left( {{u_n}} \right)\) bị chặn trên và bị chặn dưới nên dãy số \(\left( {{u_n}} \right)\) bị chặn.
Chọn A.

+) \(U_n=\sqrt{n^2+2}-n=\frac{2}{\sqrt{n^2+2}+n}\)
\(U_{n+1}=\sqrt{\left(n+1\right)^2+2}-\left(n+1\right)=\frac{2}{\sqrt{\left(n+1\right)^2+2}+n+1}\)
Vì \(\frac{2}{\sqrt{n^2+2}+n}>\frac{2}{\sqrt{\left(n+1\right)^2+2}+n+1}\)với mọi số tự nhiên n
=> \(U_n>U_{n+1}\)với mọi số tự nhiên n
=> \(U_n\) là dãy giảm.
+) Ta có: \(\sqrt{n^2+2}-n\le\sqrt{\left(n+\sqrt{2}\right)^2}-n=\sqrt{2}\)với mọi số tự nhiên n
=> \(U_n\) là dãy bị chặn

a) Bị chặn trên vì \(u_n\le1,\forall n\in\mathbb{N}^{\circledast}\)
b) Bị chặn dưới vì \(u_n\ge2,\forall n\in\mathbb{N}^{\circledast}\)
c) Bị chặn dưới vì \(u_n\ge\sqrt{3},\forall n\in\mathbb{N}^{\circledast}\)
d) Bị chặn vì \(0< u_n\le\dfrac{1}{2},\forall n\in\mathbb{N}^{\circledast}\)


Xét hiệu:
un+1−un=(n+1+1n+1)−(n+1n)=1+1n+1−1n=n2+n−1n(n+1)>0,∀n∈N∗un+1−un=(n+1+1n+1)−(n+1n)=1+1n+1−1n=n2+n−1n(n+1)>0,∀n∈N∗
Suy ra: un là dãy số tăng (1)
Mặt khác: un=n+1n≥2√n.1n=2∀n∈N∗un=n+1n≥2n.1n=2∀n∈N∗
Nên un là dãy số bị chặn dưới (2)
Ta thấy khi n càng lớn thì un càng lớn nên un là dãy số không bị chặn (3)
Từ (1), (2), (3) ta có un là dãy số tăng và bị chặn dưới.
b) Ta có:
u1 = (-1)0.sin1 = sin 1 > 0
u2=(−1)1.sin12=−sin12<0u3=(−1)2.sin13=sin13>0u2=(−1)1.sin12=−sin12<0u3=(−1)2.sin13=sin13>0
⇒ u1 > u2 và u2 < u3
Vậy un là dãy số tăng không đơn điệu.
Ta lại có:
|un|=|(−1)n−1.sin1n|=|sin1n|≤1⇔−1≤un≤1|un|=|(−1)n−1.sin1n|=|sin1n|≤1⇔−1≤un≤1
Vậy un là dãy số bị chặn và không đơn điệu.
c) Ta có:
un=√n+1−√n=n+1−n√n+1+√n=1√n+1+√nun=n+1−n=n+1−nn+1+n=1n+1+n
Xét hiệu:
un+1−un=1√(n+1)+1+√n+1−1√n+1+√n=1√n+2+√n+1−1√n+1+√nun+1−un=1(n+1)+1+n+1−1n+1+n=1n+2+n+1−1n+1+n
Ta có:
{√n+2>√n+1√n+1>√n⇒√n+2+√n+1>√n+1+√n{n+2>n+1n+1>n⇒n+2+n+1>n+1+n
⇒1√n+2+√n+1<1√n+1+√n⇒un+1−un<0⇒1n+2+n+1<1n+1+n⇒un+1−un<0
⇒ un là dãy số giảm (1)
Mặt khác:
un=1√n+1+√n>0,∀n∈N∗un=1n+1+n>0,∀n∈N∗
Suy ra: un là dãy số bị chặn dưới (2)
Ta lại có: với n ≥ 1 thì √n+1+√n≥√2+1n+1+n≥2+1
Nên un=1√n+1+√n≤1√2+1un=1n+1+n≤12+1
Suy ra: un là dãy số bị chặn trên (3)
Từ (1), (2) và (3) ta có: un là dãy số giảm và bị chặn
a)
Xét hiệu
\(u_{n+1}-u_n=\left(n+1+\dfrac{1}{n+1}\right)-\left(n+\dfrac{1}{n}\right)\)\(=1+\dfrac{1}{n+1}-\dfrac{1}{n}=1-\dfrac{1}{n\left(n+1\right)}=\dfrac{n^2+n-1}{n\left(n+1\right)}>0\) (Với mọi \(n\in N^{\circledast}\) ).
Suy ra: \(u_{n+1}>u_n\) nên \(\left(u_n\right)\) là dãy số tăng.
Mặt khác: \(u_n\ge2\sqrt{n.\dfrac{1}{n}}=2\) nên \(\left(u_n\right)\) là dãy số bị chặn dưới bởi 2.
Mặt khác n càng tăng thì \(u_n\) càng lớn theo giá trị của \(n\) nên \(\left(u_n\right)\) là dãy số không bị chặn trên.
b) \(u_1=\left(-1\right)^{1-1}.sin1=sin1>0\).
\(u_2=\left(-1\right)^{2-1}sin\dfrac{1}{2}=-sin\dfrac{1}{2}< 0\).
\(u_3=\left(-1\right)^{3-1}.sin\dfrac{1}{3}=sin\dfrac{1}{3}>0\).
Ta thấy \(u_1>u_2\) và \(u_2< u_3\) nên \(\left(u_n\right)\) là dãy số không tăng và không giảm.
\(\left|u_n\right|=\left|\left(-1\right)^{n-1}sin\dfrac{1}{n}\right|\le\left|\left(-1\right)^{n-1}\right|=1\).
Suy ra: \(-1\le u_n\le1\) nên \(\left(u_n\right)\) bị chặn trên bởi \(1\) và chặn dưới bởi \(-1\).
c)
\(u_n=\sqrt{n+1}-\sqrt{n}=\dfrac{\left(\sqrt{n+1}-\sqrt{n}\right)\left(\sqrt{n+1}+\sqrt{n}\right)}{\left(\sqrt{n+1}+\sqrt{n}\right)}\)\(=\dfrac{1}{\sqrt{n+1}+\sqrt{n}}\)
Xét hiệu:
\(u_{n+1}-u_n=\dfrac{1}{\sqrt{n+2}+\sqrt{n+1}}-\dfrac{1}{\sqrt{n+1}+\sqrt{n}}\)
\(=\dfrac{\sqrt{n}-\sqrt{n+2}}{\left(\sqrt{n+2}+\sqrt{n+1}\right)\left(\sqrt{n+1}+\sqrt{n}\right)}\)
\(=\dfrac{-2}{\left(\sqrt{n+2}+\sqrt{n+1}\right)\left(\sqrt{n+1}+\sqrt{n}\right)\left(\sqrt{n}+\sqrt{n+2}\right)}< 0\)
Vậy \(\left(u_n\right)\) là dãy số giảm.
\(u_n=\dfrac{1}{\sqrt{n+1}+\sqrt{n}}>0\) nên \(\left(u_n\right)\) là dãy số bị chặn dưới bởi 0.
\(u_n=\dfrac{1}{\sqrt{n+1}+\sqrt{n}}< \dfrac{1}{\sqrt{1+0}+\sqrt{0}}=1\) nên \(\left(u_n\right)\) là dãy số bị chặn trên bởi 1.

a)
\(u_1=1+\left(1-1\right).2^1=1\);
\(u_2=1+\left(2-1\right).2^2=1+2^2=5\);
\(u_3=1+\left(3-1\right).2^3=1+2.2^3=17\);
\(u_4=1+\left(4-1\right).2^4=1+3.2^4=49\);
\(u_5=1+\left(5-1\right).2^5=1+4.2^5=129\).
b)
\(u_n=1+\left(n-1\right).2^n\).
\(u_{n+1}=1+\left(n+1-1\right).2^{n+1}=1+n.2^{n+1}\)
\(=1+\left(n-1\right).2^{n+1}+2^{n+1}\)\(=2\left[1+\left(n-1\right).2^n\right]+2^{n+1}-1\)
\(=2.u_n+2^{n+1}-1\).
Vậy công thức truy hồi của dãy số là: \(\left\{{}\begin{matrix}u_1=1\\u_n=2u_{n-1}+2^n-1\end{matrix}\right.\).
c) Có \(u_n=1+\left(n-1\right).2^n\ge1+\left(1-1\right).2^n=1\).
Vậy \(u_n\ge1,\forall n\in N^{\circledast}\). Nên dãy \(\left(u_n\right)\) bị chặn dưới bởi 1.
Xét .
\(u_n-u_{n-1}=2u_{n-1}+2^n-1-u_{n-1}=u_{n-1}+2^n-1\)\(\ge1+2^n-1=2^n>0,\forall n\in N^{\circledast}\).
Vậy \(u_n-u_{n-1}>0,\forall n\in N^{\circledast}\) nên dãy \(\left(u_n\right)\) là dãy số tăng.

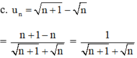
+ Xét tính tăng giảm.
Với mọi n ∈ N ta có:
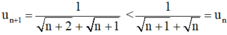
⇒ un + 1 < un với mọi n ∈ N.
⇒ (un) là dãy số giảm.
+ Xét tính bị chặn.
un > 0 với mọi n.
⇒ (un) bị chặn dưới.
un ≤ u1 = √2 - 1 với mọi n
⇒ (un) bị chặn trên.
⇒ (un) bị chặn.

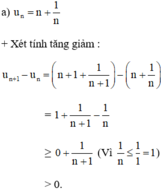
⇒ un + 1 > un với mọi n ∈ N
⇒ (un) là dãy tăng.
+ Xét tính bị chặn:
(un) là dãy tăng
⇒ u1 = 2 < u2 < u3 < …< un ∀n ∈ N*
⇒ un ≥ 2 ∀n ∈ N*
⇒ (un) bị chặn dưới.
(un) không bị chặn trên.
⇒ un không bị chặn.

Ta có: u n > 0 ∀ n ≥ 1
u n + 1 u n = n 2 + n + 1 ( n + 1 ) 2 + ( n + 1 ) + 1 = n 2 + n + 1 n 2 + 3 n + 3 < 1 ∀ n ∈ ℕ *
⇒ u n + 1 < u n ∀ ≥ 1 ⇒ dãy ( u n ) là dãy số giảm.
Mặt khác: 0 < u n < 1 ⇒ dãy ( u n ) là dãy bị chặn.
Chọn đáp án C
Ta có: u n = 2 ( n + 1 ) − 13 3 ( n + 1 ) − 2 = 2 n − 11 3 n + 1
Xét hiệu:
u n + 1 − u n = 2 n − 11 3 n + 1 − 2 n − 13 3 n − 2 = ( 2 n − 11 ) . ( 3 n − 2 ) − ( 2 n − 13 ) . ( 3 n + 1 ) ( 3 n + 1 ) ( 3 n − 2 ) = 6 n 2 − 4 n − 33 n + 22 − ( 6 n 2 + 2 n − 39 n − 13 ) ( 3 n + 1 ) . ( 3 n − 2 ) = 35 ( 3 n + 1 ) ( 3 n − 2 ) > 0
với mọi n ≥ 1 .
Suy ra u n + 1 > u n ∀ n ≥ 1 ⇒ dãy ( u n ) là dãy tăng.
Mặt khác: u n = 2 3 − 35 3 ( 3 n − 2 ) ⇒ u n < 2 3 ∀ n ≥ 1
Suy ra u n bị chặn trên
∀ n ≥ 1 : 3 n − 2 ≥ 1 ⇒ 35 3 ( 3 n − 2 ) ≤ 35 3.1 = 35 3 ⇒ u n ≥ 2 3 − 35 3 = − 11
Nên ( u n ) bị chặn dưới.
Vậy dãy ( u n ) là dãy bị chặn.
Chọn đáp án A.