
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

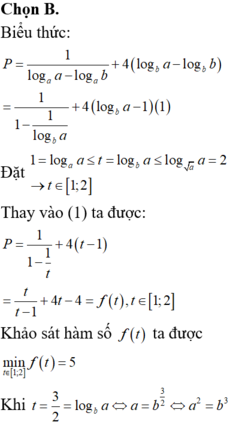

Đáp án A
Ta có log a b b = log a b a . b a = log a b a − 1 .
Do đó
P = 2 2 log a b a − log a b a − 1 2 + 27 log a b a = 2 log a b a + 1 2 + 27 log a b a .
Đặt t = log a b a . Do 1 < a ≤ b 2 ⇒ a ≤ b .
Suy ra
1 t = 1 log a b a = log a a b = 1 − log a b ≤ 1 − log a a = 1 − 1 2 = 1 2 ⇒ t ≥ 2
Khi đó P = 2 t + 1 2 + 27 t = f t .
Khảo sát f t trên 2 ; + ∞ , ta được f t đạt giá trị nhỏ nhất bằng 63 2 khi t=2.
Với t = 2 ⇒ log a b a = 2 ⇔ a = b 2 .

Dễ dàng biến đổi được ![]()
Từ điều kiện, suy ra a > 1
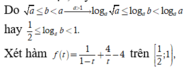 ta được f(t) đạt giá trị nhỏ nhất bằng 5 khi
ta được f(t) đạt giá trị nhỏ nhất bằng 5 khi ![]()
Chọn B.

Đáp án D
Đặt 0 < t = log a b ≤ 1
⇒ P = log a a b + log a a + log a b = 1 + t + 1 − t = f t
f ' t = 1 − 1 2 1 − t → f ' t = 0
⇔ t = 3 4 ⇒ f 3 4 = 9 4 .
Dựa vào bảng biến thiên,
suy ra f t 0 < t ≤ 1 ≤ f 3 4
Khi đó t = 3 4 = log a b
⇔ a 3 4 = b ⇔ k = 3 4