Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Không gian mẫu gồm các hoán vị của 6 người. Vậy n(Ω) = 6!
Kí hiệu A là biến cố : " Đứa bé được xếp giữa hai người đàn bà ";
B là biến cố : " Đứa bé được xếp giữa hai người đàn ông ".
a) Để tạo nên một cách xếp mà đứa bé được xếp giữa hai người đàn bà, ta tiến hành như sau :
- Xếp đứa bé ngồi vào ghế thứ hai đến ghế thứ năm. Có 4 cách.
- Ứng với mỗi cách xếp đứa bé, có 2 cách xếp hai người đàn bà.
- Khi đã xếp hai người đàn bà và đứa bé, xếp ba người đàn ông vào các chỗ còn lại. Có 3! cách.
Theo quy tắc nhân, ta có n(A) = 4.2.3! = 48.
Từ đó: 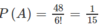
b) Để tạo nên một cách xếp mà đứa bé ngồi giữa hai người đàn ông, ta tiến hành như sau :
- Xếp đứa bé vào các ghế thứ hai đến thứ năm. Có 4 cách.
- Chọn hai trong số ba người đàn ông. Có 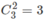 cách.
cách.
- Xếp hai người đàn ông ngồi hai bên đứa bé. Có 2 cách.
- Xếp ba người còn lại vào ba chỗ còn lại. Có 3! cách. Theo quy tắc nhân, ta có
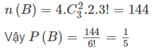

Đáp án là D.
• Số phần tử không gian mẫu n ( Ω ) = 6 !
• Gọi biến cố A" đứa bé ngồi giữa hai người đàn bà".
+ Xếp 2 người đàn bà ngồi 2 bên đứa bé có: 2! cách
+ Xem 2 người đàn bà và đứa bé là 1 vị trí sắp xếp với 3 người đàn ông còn lại có: 4! cách
+ Số phần tử của A: n(A) = 2!.4!
Xác suất cần tìm P ( A ) = 2 ! . 4 ! 6 ! = 1 15

2, sin4x+cos5=0 <=> cos5x=cos\(\left(\frac{\pi}{2}+4x\right)\Leftrightarrow\orbr{\begin{cases}x=\frac{\pi}{2}+k2\pi\\x=-\frac{\pi}{18}+\frac{k2\pi}{9}\end{cases}\left(k\inℤ\right)}\)
ta có \(2\pi>0\Leftrightarrow k< >\frac{1}{4}\)do k nguyên nên nghiệm dương nhỏ nhất trong họ nghiệm \(\frac{\pi}{2}\)khi k=0
\(-\frac{\pi}{18}+\frac{k2\pi}{9}>0\Leftrightarrow k>\frac{1}{4}\)do k nguyên nên nghiệm dương nhỏ nhất trong họ nghiệm \(-\frac{\pi}{18}-\frac{k2\pi}{9}\)là \(\frac{\pi}{6}\)khi k=1
vậy nghiệm dương nhỏ nhất của phương trình là \(\frac{\pi}{6}\)
\(\frac{\pi}{2}+k2\pi< 0\Leftrightarrow k< -\frac{1}{4}\)do k nguyên nên nghiệm âm lớn nhất trong họ nghiệm \(\frac{\pi}{2}+k2\pi\)là \(-\frac{3\pi}{2}\)khi k=-1
\(-\frac{\pi}{18}+\frac{k2\pi}{9}< 0\Leftrightarrow k< \frac{1}{4}\)do k nguyên nên nghiệm âm lớn nhất trong họ nghiệm \(-\frac{\pi}{18}+\frac{k2\pi}{9}\)là \(-\frac{\pi}{18}\)khi k=0
vậy nghiệm âm lớn nhất của phương trình là \(-\frac{\pi}{18}\)



Đáp án D
Số cách xếp 6 người thành hàng ngang là: 6!
Coi 2 người đàn bà là 1 thì số cách sắp xếp người lớn là:4!=24
Hai người đàn bà đổi chỗ cho nhau ta được một trường hợp riêng nên số cách xếp người lớn là
2.4!=48
ứng với mỗi cách xếp người lớn chỉ có một cách xếp trẻ con nên số cách để xếp 1 đứa trẻ ngồi giữa hai người đàn bà là: 48
⇒ n = 48 6 ! = 1 5