Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

HD: Xếp 10 quyển sách tham khảo thành một hàng ngang trên giá sách có : 10! cách sắp xếp.
Sắp xếp 2 cuốn toán 1 và toán 2 cạnh nhau có 2! cách,
Sắp xếp 6 cuốn sách Toán sao cho có hai quyển Toán T1 và Toàn T2 cạnh nhau có 2!.5! cách.
Khi đó có 4 vị trí để sắp xếp 3 cuốn Anh ở giữa hai quyển Toán và 3 cách sắp xếp cuốn Tiếng Anh.
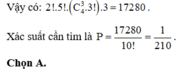

Đáp án C
Phương pháp giải: Sử dụng biến cố đối và các quy tắc đếm cơ bản.
Lời giải:
Chọn 3 quyển sách trong 15 quyển sách có ![]() cách => n(Ω) = 455
cách => n(Ω) = 455
Gọi X là biến cố 3 quyển sách được lấy ra có ít nhất một quyển sách là toán.
Và X là biến cố 3 quyển sách được lấy ra không có quyển sách toán. Khi đó, ta xét các trường hợp sau:
TH1. Lấy được 2 quyển lý, 1 quyển hóa => có ![]() cách
cách
TH2. Lấy được 1 quyển lý, 2 quyển hóa => có ![]() cách
cách
TH3. Lấy được 3 quyển lý, 0 quyển hóa => có ![]() cách
cách
TH4. Lấy được 0 quyển lý, 3 quyển hóa => có ![]() cách
cách
Suy ra số phần tử của biến cố
X
là 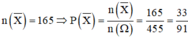
Vậy xác suất cần tính là ![]()

Trả lời: Gọi giá một quyển sách, một quyển vở, một chiếc bút thứ tự là S, V, B đồng. Ta có:
\(S+6V+3B=7700\) (1)
\(8S+6V+6B=16000\) (2)
Nhân (1) với 2 rồi trừ vào (2) ta được:
\(6S-6V=600=>S-V=100\)
Giá một quyển sách nhiều hơn giá một quyển

Đáp án A
Số phần tử của không gian mẫu n Ω = C 9 3 = 84
Gọi A là biến cố sao cho ba quyển lấy ra có
ít nhất một quyển sách Toán. ⇒ n A ¯ = C 5 3 = 10
⇒ A ¯ là biến cố sao cho ba quyển lấy ra không
có sách Toán ⇒ n A ¯ = C 5 3 = 10 .
⇒ P A = 1 − P A ¯ = 1 − 10 84 = 37 42

Chọn đáp án C.
Số kết quả có thể khi chọn bất kì 3 quyển sách trong 9 quyển sách là C 9 3 = 84 .
Gọi A là biến có “Lấy được ít nhất 1 sách toán trong 3 quyển sách.”
A là biến cố “Không lấy được sách toán trong 3 quyển sách.”
Ta có xác suất để xảy ra A là P A = 1 - P A = 1 - C 5 3 84 = 37 42 .

Đáp án C
Lấy ngẫu nhiên 3 cuốn sách có: C 9 3 = 84 cách
Gọi A là biến cố: Lấy 3 cuốn sách và không có cuốn nào là cuốn toán
Suy ra A ¯ là biến cố: 3 quyển được lấy ra có ít nhất một quyển là toán
Khi đó Ω A = C 5 3 = 10 .
Vậy p A = Ω A Ω = 10 84 = 5 42 ⇒ p A ¯ = 1 − p A = 37 42



Đáp án A
Phương pháp giải: Áp dụng các quy tắc đếm cơ bản trong bài toán sắp xếp đồ vật
Lời giải: Xếp 5 quyển Toán (coi Toán T1 và Toán T2 là một) có 5 ! .2 ! = 240 cách.
Khi đó, sẽ tạo ra 4 khoảng trống kí hiệu như sau: _T_T_T_T_T_
Xếp 3 quyển sách Tiếng Anh vào 4 khoảng trống giữa hai quyển toán có A 4 3 cách.
Xếp 1 quyển sách Văn vào 3 vị trí còn lại có 3 cách.
Vậy xác suất cần tính là P = 240. A 4 3 .3 10 ! = 1 210 .