PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NN
0
NN
0
16 tháng 6 2019
a, ĐK \(\hept{\begin{cases}a\ge1\\a\le-1\end{cases}}\)
b, ĐK a\(\le\)2
KN
16 tháng 6 2019
a) Ta có: \(\sqrt{a^2-1}=\sqrt{\left(a+1\right)\left(a-1\right)}\)
Để \(\sqrt{a^2-1}\) có nghĩa thì \(\left(a+1\right)\left(a-1\right)\ge0\)
\(\Leftrightarrow\orbr{\begin{cases}a+1\le0\\a-1\ge0\end{cases}}\Leftrightarrow\orbr{\begin{cases}a\le-1\\a\ge1\end{cases}}\)
TH
1
17 tháng 9 2020
\(\sqrt{-\left|x+5\right|}\)có nghĩa khi và chỉ khi \(-\left|x+5\right|\ge0\Leftrightarrow\left|x+5\right|\le0\)
Mà\(\left|x+5\right|\)là không âm nên đề bài thỏa mãn khi và chỉ khi \(\left|x+5\right|=0\Leftrightarrow x=-5\)
CM
11 tháng 12 2017
a)
Điều kiện xác định của a 3 là
a 3 ≥ 0 ⇒ a ≥ 0
b) Điều kiện -5a ≥ 0 => a ≤ 0
c) Điều kiện 4 – a ≥ 0 => -a ≥ -4 = > a ≤ 4
d) Điều kiện 3a + 7 ≥ 0 => 3a ≥ -7
a ≥ - 7 3
NN
0
PT
1
PT
1
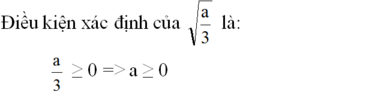
Điều kiện 3a + 7 ≥ 0 => 3a ≥ -7
⇒ a ≥ - 7 3