Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét mặt phẳng (P) đi qua d và (P) ⊥ (Oxy), khi đó ∆ = (P) ∩ (Oxy) chính là hình chiếu vuông góc của d lên mặt phẳng (Oxy).
Phương trình mặt phẳng (Oxy) có dạng: z = 0 ; vectơ (0 ; 0 ;1) là vectơ pháp tuyến của (Oxy), khi đó
và
( 1 ; 2 ; 3) là cặp vectơ chỉ phương của mặt phẳng (P).
= (2 ; -1 ; 0) là vectơ pháp tuyến của (P).
Phương trình mặt phẳng (P) có dạng:
2(x - 2) - (y + 3) +0.(z - 1) = 0
hay 2x - y - 7 = 0.
Đường thẳng hình chiếu ∆ thỏa mãn hệ:
Điểm M0( 4 ; 1 ; 0) ∈ ∆ ; vectơ chỉ phương của ∆ vuông góc với
và vuông góc với
, vậy có thể lấy
= (1 ; 2 ; 0).
Phương trình tham số của hình chiếu ∆ có dạng:
.
Chú ý :
Ta có thể giải bài toán này bằng cách sau:
Lấy hai điểm trên d và tìm hình chiếu vuông góc của nó trên mặt phẳng (Oxy). Đường thẳng đi qua hai điểm đó chính là hình chiếu cần tìm.
Chẳng hạn lấy M1( 2 ; 3 ; -1) ∈ d và M2( 0 ; -7 ; -5) ∈ d, hình chiếu vuông góc của
M1 trên (Oxy) là N1 (2 ; -3 ; 0), hình chiếu vuông góc của M2 trên (Oxy) là N2(0 ; -7 ; 0).
Đườn thẳng ∆ qua N1, N2 chính là hình chiếu vuông góc của d lên (Oxy).
Ta có : (-2 ; -4 ; 0) //
(1 ; 2 ; 0).
Phương trình tham số của ∆ có dạng:
.
b) Tương tự phần a), mặt phẳng (Oxy) có phương trình x = 0.
lấy M1( 2 ; 3 ; -1) ∈ d và M2( 0 ; -7 ; -5) ∈ d, hình chiếu vuông góc của
M1 trên (Oxy) là M'1 (0 ; -3 ; 1), hình chiếu vuông góc của M2 trên (Oyz) là chính nó.
Đườn thẳng ∆ qua M'1, M2 chính là hình chiếu vuông góc của d lên (Oyz).
Ta có: (0 ; -4 ; -6) //
(0 ; 2 ; 3).
Phương trình M'1M2 có dạng:
.

Hình chiếu của M trên (Oyz) là : M 1 (0 ; -3 ; 1)
Hình chiếu của N trên (Oyz) là : N 1 (0 ; -1 ; 4)
⇒ Hình chiếu của d trên (Oyz) chính là đường thẳng d 1 đi qua M 1 và N 1
⇒ d1 nhận 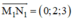 là 1 vtcp
là 1 vtcp
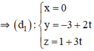

Đường thẳng d đi qua A (1; 1; 9) và có vectơ chỉ phương \(\overrightarrow{a}\left(1;1;0\right)\). Gọi (Q) là mặt phẳng đi qua d và vuông góc với (P)


Đáp án D
Gọi M(1+2t;2t;2-t) là giao điểm của d và (Oxy): z =0
![]()
Gọi N(1;0;2) là điểm thuộc d. Hình chiếu của N lên (Oxy) là I(1;0;0)
![]()
là một véc tơ chỉ phương của d’

a) Gọi \(\overrightarrow{u}\left(1;-2;-1\right)\) là vectơ chỉ phương của d, giả sử \(\overrightarrow{v}\left(a;b;c\right)\) là 

Đáp án C
Hình chiếu của A,B trên mp (Oxy) là A'(1;0;0); B'(3;-1;0). Có A B → = ( 2 ; - 1 ; 0 ) là vtcp của A’B’ nên phương trình tham số của A’B’ là
x = 1 + 2 t y = - t z = 0
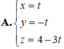
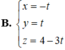
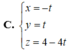
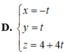



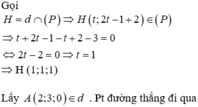

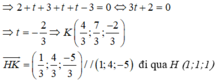


+ t = 0 ⇒ điểm M(2; -3; 1) ∈ d
+ t = 1 ⇒ điểm N(3; -1; 4) ∈ d.
Hình chiếu của M trên (Oxy) là M’(2 ; -3 ; 0).
Hình chiếu của N trên (Oxy) là : N’(3 ; -1 ; 0).
⇒ Hình chiếu của d trên (Oxy) chính là đường thẳng d’ đi qua M’ và N’.
⇒ d’ nhận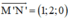 là 1 vtcp.
là 1 vtcp.