K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
23 tháng 9 2017
Chọn C
Số hạng tổng quát trong khai triển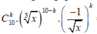 
.
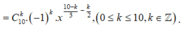Số hạng không chứa x ứng với k thỏa mãn: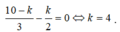 
.
Vậy số hạng không chứa x cần tìm: 
.
LT
3 tháng 4 2017
a) Theo dòng 5 của tam giác Pascal, ta có:
(a + 2b)5= a5 + 5a4 (2b) + 10a3(2b)2 + 10a2 (2b)3 + 5a (2b)4 + (2b)5
= a5 + 10a4b + 40a3b2 + 80a2b3 + 80ab4 + 32b5
b) Theo dòng 6 của tam giác Pascal, ta có:
(a - √2)6 = [a + (-√2)]6 = a6 + 6a5 (-√2) + 15a4 (-√2)2 + 20a3 (-√2)3 + 15a2 (-√2)4 + 6a(-√2)5 + (-√2)6.
= a6 - 6√2a5 + 30a4 - 40√2a3 + 60a2 - 24√2a + 8.
c) Theo công thức nhị thức Niu – Tơn, ta có:
(x - )13= [x + (-
)]13 =
Ck13 . x13 – k . (-
)k =
Ck13 . (-1)k . x13 – 2k
Nhận xét: Trong trường hợp số mũ n khá nhỏ (chẳng hạn trong các câu a) và b) trên đây) thì ta có thể sử dụng tam giác Pascal để tính nhanh các hệ số của khai triển.
CM
3 tháng 6 2017
Chọn D
Xét khai triển nhị thức Niutơn:
(
2
x
-
1
)
6
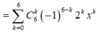
Số hạng chứa x 3 trong khai triển ứng với k = 3.
Vậy hệ số của số hạng chứa
x
3
trong khai triển là: 
.
PT
1
PT
1
PT
1
20 tháng 10 2017
\(\left(a+b\right)^n=a^n+C^1_na^{n-1}b+C^2_na^{n-2}b^2+...+C^{n-1}_nab^{n-1}+b^n\)
=> \(\left(\sqrt{3}+\sqrt[3]{30}\right)^6=\sqrt{3}^6+C^1_6\sqrt{3}^5\cdot\sqrt[3]{30}+C^2_6\sqrt{3}^4\cdot\sqrt[3]{30}^2+C_6^3\sqrt{3}^3\cdot\sqrt[3]{30}^3+C^4_6\sqrt{3}^2\cdot\sqrt[3]{30}^4+C^5_6\sqrt{3}\cdot\sqrt[3]{30}^5+\sqrt[3]{30}^6\)
...muộn rồi, tự làm nốt nhé :))...
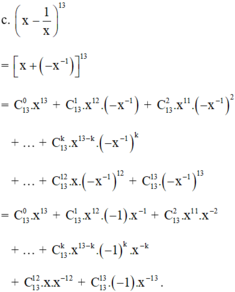
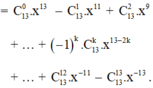
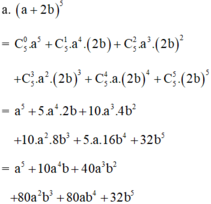
Công thức nhị thức Niutơn:
(a+b)n = Cn0 an + Cn1an-1 b + … Cnkan-k bk + ... + Cnn-1a bn-1 + Cnn bn.
Chú ý: số hạng T(k+1) =Cnk a(n-k)bk được gọi là số hạng tổng quát của khái triển (a+b)n.