
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bước 1: Vẽ cạnh NP nằm ngang bằng 3 cm.
Bước 2: Sử dụng com-pa với độ mở là 2,5 cm, vẽ đường tròn tâm N bán kình 2,5 cm.
Sử dụng com-pa với độ mở là 5 cm, vẽ đường tròn tâm P bán kính 5 cm.
Giao điểm của đường tròn tâm N bán kính 2,5 cm và đường tròn tâm P bán kính 5 cm chính là điểm M cần tìm.
Bước 3: Nối M với N, M với P, ta có tam giác MNP cần dựng.
Mình không vẽ bằng máy được nên hướng dẫn bạn cách vẽ, bạn thông cảm nhé!


a: NP^2=MN^2+MP^2
=>ΔMNP vuông tại M
b: Xét ΔNMD vuông tại M và ΔNED vuông tại E có
ND chung
góc MND=góc END
=>ΔNMD=ΔNED
=>DM=DE

Cho tam giác ABC bằng tam giác MNP. Biết AB+BC=11 cm, MN-NP= 3 cm. Khi đó MN= 7 cm.

Đối diện cạnh MN là góc P
Đối diện cạnh NP là góc M
Đối diện cạnh MP là góc NMà MP>NP>MN(6cm>5cm>4cm)=>góc N>M>P
M P N 3 4 A C G
a) xét \(\Delta MNP\)VUÔNG TẠI M CÓ
\(\Rightarrow NP^2=MN^2+MP^2\left(PYTAGO\right)\)
THAY\(NP^2=4^2+3^2\)
\(NP^2=16+9\)
\(NP^2=25\)
\(\Rightarrow NP=\sqrt{25}=5\left(cm\right)\)
XÉT \(\Delta MNP\)CÓ
\(\Rightarrow NP>MN>MP\left(5>4>3\right)\)
\(\Rightarrow\widehat{M}>\widehat{P}>\widehat{N}\)( QUAN HỆ GIỮA CẠNH VÀ GÓC ĐỐI DIỆN)
B) xét \(\Delta\text{ CPM}\)VÀ\(\Delta\text{CPA}\)CÓ
\(PM=PA\left(GT\right)\)
\(\widehat{MPC}=\widehat{APC}=90^o\)
PC LÀ CAH CHUNG
=>\(\Delta\text{ CPM}\)=\(\Delta\text{CPA}\)(C-G-C)
c)
\(\Delta CPM=\Delta CPA\left(cmt\right)\)
\(\Rightarrow\widehat{CMP}=\widehat{CPA}\left(\text{hai góc tương ứng}\right)\)
\(\text{Ta có: }\)\(\widehat{MNA}+\widehat{NAM}=90^o\left(\Delta MNA\perp\text{ tại M}\right)\)
\(\widehat{NMC}+\widehat{CMP}=90^o\)
\(\Rightarrow\widehat{MNA}+\widehat{NAM}=\)\(\widehat{NMC}+\widehat{CMP}\)
\(\Rightarrow\widehat{MNA}=\widehat{NMC}\left(\widehat{CMP}=\widehat{NAM}\right)\)
\(Hay:\)\(\widehat{MNC}=\widehat{NMC}\)
\(\Rightarrow\Delta NMC\text{ cân}\)
\(\Rightarrow CN=CM\left(đpcm\right)\)

ta có : tam giác MNP=tam giácEFG
=>MN=EF; NP=FG; MP=EG
=>EG=3cm ; EF+FG=7cm ; FG-FE=1cm
=>FG > EF 1cm mà EF + FG=7cm
=>FG=4cm;EF=3cm
Chu vi tam giác EFG là:
4+3+3=10(cm)
Vậy chu vi tam giác EFG=10cm
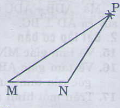
- Vẽ đoạn thẳng MN = 2,5cm.
- Trên cùng một nửa mặt phẳng bờ MN vẽ cung tròn tâm M bán kính 5cm, và cung tròn tâm N bán kính 3cm
- Hai cung tròn cắt nhau tại P. Vẽ các đoạn thẳng MP, NP ta được tam giác MNP.