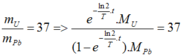Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Cứ 1 hạt nhân \(_{92}^{238}U\) bị phân rã tạo ra 1 hạt nhân \(_{82}^{206}Pb\). Từ đó ta có nhận xét là số hạt nhân \(_{92}^{238}U\) bị phân rã chính bằng số hạt nhân \(_{82}^{206}Pb\) tạo thành.
Tỉ số giữa số hạt nhân \(_{92}^{238}U\) bị phân rã và số hạt nhân \(_{92}^{238}U\) còn lại là
\(\frac{\Delta N}{N}= \frac{6,239.10^{18}}{1,188.10^{20}}= 0,0525 = \frac{1-2^{-\frac{t}{T}}}{2^{-\frac{t}{T}}}\)
Nhân chéo => \(2^{-\frac{t}{T}}= 0,95.\)
=> \(t = -T\ln_2 0,95 = 3,3.10^8\)(năm)
=> Tuổi của khối đã là 3,3.108 năm.
Kí hiệu \(N_{01}\), \(N_{02}\) là số hạt ban đầu lần lượt của \(^{235}U\) và \(^{238}U\).
t = 0 Ban đầu t thời điểm cần xác định hiện nay t 1 2
Hiện nay \(t_2\): \(\frac{N_{1}}{N_{2}}=\frac{N_{01}2^{-\frac{t_2}{T_1}}}{N_{02}2^{-\frac{t_2}{T_2}}} =\frac{7}{1000}.(1)\)
Thời điểm \(t_1\):
\(\frac{N_1}{N_2}= \frac{N_{01}2^{-\frac{t_1}{T_1}}}{N_{02}2^{-\frac{t_1}{T_2}}} = \frac{3}{100}.(2)\)
Chia (1) cho (2) => \(\frac{2^{-\frac{t_2}{T_1}}.2^{-\frac{t_1}{T_2}}}{2^{-\frac{t_1}{T_1}}.2^{-\frac{t_2}{T_2}}}= \frac{7.100}{3.1000}= \frac{7}{30}.\)
Áp dụng \(\frac{1}{2^{-x}} =2^x. \)
=> \(2^{(t_2-t_1)(\frac{1}{T_2}-\frac{1}{T_1})} = \frac{7}{30}.\)
=> \(t_2-t_1 = \frac{T_1T_2}{T_1-T_2}\ln_2 (7/30)=1,74.10^{9}\).(năm) \(= 1,74 \)(tỉ năm).
Như vậy cách hiện nay 1,74 tỉ năm thì trong urani tự nhiên có tỉ lệ số hạt thỏa mãn như bài cho.
\(_{92}^{238}U \rightarrow _2^4He + _{90}^{234}\text{Th}\)
Sau 9.109 năm thì số gam Urani bị phân rã là
\(\Delta m = m_0 - m(t) = m_0(1-2^{-t/T}) = 6,97g.\)
Số mol urani bị phân rã là \(n = \frac{\Delta m}{A_{U}} = \frac{6,97}{238} = 0,0293 \text{mol}.\)
Dựa vào phương trình ta thấy cứ 1 hạt Urani bị phân rã sẽ tạo thành 1 hạt Thori. Suy ra \(n_{Th} = n_{urani}\)
Nhưu vậy khối lượng Thori tạo thành là \(m_{Th} = 0,0293.234 = 6,854 g.\)
Do hạt nhân mẹ Po ban đầu đứng yên, áp dụng định luật bảo toàn động lượng trước và sau phản ứng ta thu được
\(P_{\alpha} = P_{Pb} \)
=> \(2m_{\alpha} K_{\alpha}=2m_{Pb}K_{Pb} \)
=> \( 4,0026.K_{\alpha}=205,9744.K_{Rn}.(1)\)
Áp dụng định luật bảo toàn năng lượng toàn phần có
\(K_{\alpha}+K_{Pb} = (m_t-m_s)c^2\)
=> \(K_{\alpha}+K_{Rn} = (m_{Po}-m_{\alpha}-m_{Pb})c^2= 0,0058.931,5 = 5,4027 MeV. (2)\)
Từ (1) và (2) giải hệ phương trình ta được
\(K_{\alpha} = 5,2997 MeV; K_{Pb} = 0,103 MeV. \)
=> \(v_{Pb}= \sqrt{\frac{2K_{Pb}}{m_{Pb}}} =\sqrt{\frac{2.0,103.10^6.1,6.10^{-19}}{205,9744.1,66055.10^{-27}}} = 3,06.10^5m/s.\)
Chú ý đổi đơn vị \(1 MeV = 10^6.1,6.10^{-19}J ; 1 u = 1,66055.10^{-27} kg.\)
Tỉ lệ khối lượng chì tạo thành và khối lượng U còn lại được xác định bởi
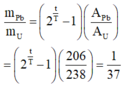
Giải phương trình trên ta thu được: t = 2 . 10 8 năm
Đáp án B
Gia tốc cực đại: \(a_{max}=\omega^2.A=(2\pi.2,5)^2.0,05=12,3m/s^2\)
Số hạt nhân Natri là \(N_0 = nN_Á = \frac{m}{A}N_A\)
Độ phóng xạ ban đầu \(H_0 = \lambda N_0 = \frac{\ln 2}{T}\frac{m}{A}N_A= 6,73.10^{16}.(Bq)\)
Chú ý là trong khi tính độ phóng xạ theo đơn vị "Bq" thì chu kì phải đổi sang đơn vị "giây" .
Cứ mỗi hạt nhân Pôlôni bị phân rã tạo thành 1 hạt nhân chì trong mẫu.
Số hạt nhân Pôlôni bị phân rã là \(\Delta N = N_0 2^{-\frac{t}{T}}.\)
Số hạt nhân Pônôni còn lại là \( N = N_0 2^{-\frac{t}{T}}.\)
Tại thời điểm t1 : \(\frac{\Delta N}{N } = \frac{1-2^{-\frac{t_1}{T}}}{2^{-\frac{t_1}{T}}}= \frac{1}{3}\)
=> \(3(1-2^{-\frac{t_1}{T}})= 2^{-\frac{t_1}{T}}\)
=> \(2^{-\frac{t_1}{T}}= 2^{-2}\)
=> \(t_1 = 2T\)
=> \(t_2 = 2T+276 = 552 \) (ngày)
=> \(\frac{t_2}{T}= \frac{552}{138}= 4.\)
Tại thời điểm t2 : \(\frac{\Delta N_1}{N_1 } = \frac{1-2^{-\frac{t_2}{T}}}{2^{-\frac{t_2}{T}}}= \frac{1-2^{-4}}{2^{-4}}= 15.\)
=> \(\frac{N_1}{\Delta N_1} = \frac{1}{15}.\)
Cứ 1 hạt Urani phân rã thì tạo thành 1 hạt Pb
Như vậy số mol Unrani bị phân rã = số mol Pb tạo thành. Gọi \(\Delta m = m_0 -m(t) = m_0.2^{-t/T}\) là khối lượng urani bị phân rã.
Ta có khối lượng Pb tạo thành là
\(m_{Pb} = n_{Pb}.A_{Pb} = \frac{\Delta m_{Urani}}{A_{Ur}}.A_{Pb}. \)
Ta có tỉ lệ khối lượng Urani còn lại và khối lượng Pb sinh ra là
\(\frac{m_{Urani}}{m_{Pb}} = \frac{m_o.2^{-t/T}}{\Delta m .206/238} =\frac{238.m_o.2^{-t/T}}{\Delta m .206} = 37 \)
=> \(\frac{m_o.2^{-t/T}.238}{m_0(1-2^{-t/T}) .206} = 37. \)
=> \(238.2^{-t/T} = 7622.(1-2^{-t/T}).\)
=> t = 2,04.108 năm.
Như vậy tuổi của đã là t = 2,04.108 năm.
Đáp án: A.
Số hạt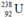
còn lại: 
Số hạt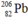
sinh ra = số hạt 
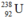phân rã:
Mặt khác:
