NT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
25 tháng 4 2018
Lời giải:
Ta có:
\((\sqrt{n+1}+\sqrt{n})U_n=\frac{2}{2n+1}\)
\(\Rightarrow U_n=\frac{2}{(2n+1)(\sqrt{n+1}+\sqrt{n})}=\frac{2(\sqrt{n+1}-\sqrt{n})}{2n+1}\)
\(=\frac{2(\sqrt{n+1}-\sqrt{n})}{(n+1)+n}<\frac{2(\sqrt{n+1}-\sqrt{n})}{2\sqrt{n(n+1)}}\) (áp dụng bđt am-gm thì \((n+1)+n\geq 2\sqrt{n(n+1)}\), dấu bằng không xảy ra vì \(n\neq n+1\))
hay \(U_n< \frac{1}{\sqrt{n}}-\frac{1}{\sqrt{n+1}}\)
Do đó:
\(U_1+U_2+...+U_{2010}< \frac{1}{\sqrt{1}}-\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{3}}+\frac{1}{\sqrt{3}}-...+\frac{1}{\sqrt{2010}}-\frac{1}{\sqrt{2011}}\)
\(\Leftrightarrow U_1+U_2+..+U_{2010}< 1-\frac{1}{\sqrt{2011}}< \frac{1005}{1006}\)
Ta có đpcm.
MH
9 tháng 4 2017
a) Năm số hạng đầu của dãy số là 3, √10, √11, √12, √13.
b) Ta có: u1 = 3 = √9 = √(1 + 8)
u2 = √10 = √(2 + 8)
u3 = √11 = √(3 + 8)
u4 = √12 = √(4 + 8)
...........
Từ trên ta dự đoán un = √(n + 8), với n ε N* (1)
Chứng minh công thức (1) bằng phương pháp quy nạp:
- Với n = 1, rõ ràng công thức (1) là đúng.
- Giả sử (1) đúng với n = k ≥ 1, tức là có uk = √(k + 8) với k ≥ 1.
Theo công thức dãy số, ta có:
uk+1 = .
Như vậy công thức (1) đúng với n = k + 1.
MH
9 tháng 4 2017
a) Năm số hạng đầu của dãy số là 3, √10, √11, √12, √13.
b) Ta có: u1 = 3 = √9 = √(1 + 8)
u2 = √10 = √(2 + 8)
u3 = √11 = √(3 + 8)
u4 = √12 = √(4 + 8)
...........
Từ trên ta dự đoán un = √(n + 8), với n ε N* (1)
Chứng minh công thức (1) bằng phương pháp quy nạp:
- Với n = 1, rõ ràng công thức (1) là đúng.
- Giả sử (1) đúng với n = k ≥ 1, tức là có uk = √(k + 8) với k ≥ 1.
Theo công thức dãy số, ta có:
uk+1 = .
Như vậy công thức (1) đúng với n = k + 1.
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 11 2018
Ta phân tích \(n^2=\dfrac{1}{3}\left(n+1\right)^3-\dfrac{1}{2}\left(n+1\right)^2+\dfrac{1}{6}\left(n+1\right)-\dfrac{1}{3}n^3+\dfrac{1}{2}n^2-\dfrac{1}{6}n\)
\(\Rightarrow u_{n+1}-\dfrac{1}{3}\left(n+1\right)^3+\dfrac{1}{2}\left(n+1\right)^2-\dfrac{1}{6}\left(n+1\right)=u_n-\dfrac{1}{3}n^3+\dfrac{1}{2}n^2-\dfrac{1}{6}n\)
Đặt \(v_n=u_n-\dfrac{1}{3}n^3+\dfrac{1}{2}n^2-\dfrac{1}{6}n\Rightarrow\left\{{}\begin{matrix}v_1=1-\dfrac{1}{3}+\dfrac{1}{2}-\dfrac{1}{6}=1\\v_{n+1}=v_n\end{matrix}\right.\)
Từ \(v_{n+1}=v_n\Rightarrow v_{n+1}=v_n=v_{n-1}=...=v_1=1\)
\(\Rightarrow u_n-\dfrac{1}{3}n^3+\dfrac{1}{2}n^2-\dfrac{1}{6}n=1\Rightarrow u_n=\dfrac{1}{3}n^3-\dfrac{1}{2}n^2+\dfrac{1}{6}n+1\)
\(\Rightarrow u_n=1+\dfrac{2n^3-3n^2+n}{6}=1+\dfrac{n\left(n-1\right)\left(2n-1\right)}{6}\)
CM
21 tháng 9 2019
a. Năm số hạng đầu của dãy số
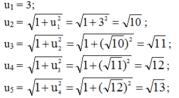
b. Dự đoán công thức số hạng tổng quát của dãy số:
un =√(n+8) (1)
Rõ ràng (1) đúng với n = 1
Giả sử (1) đúng với n = k, nghĩa là uk = √(k+8)
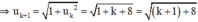
⇒ (1) đúng với n = k + 1
⇒ (1) đúng với mọi n ∈ N*.
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 12 2020
Dễ dàng nhận ra dãy đã cho là dãy dương.
\(\Rightarrow u_1u_2...u_{n-1}>0\Rightarrow u_n>1\) ;\(\forall x>1\)
\(\Rightarrow u_1u_2...u_{n-1}>1\)
Ta có:
\(u_{n+1}-u_n=1+u_1u_2...u_n-u_n=1+u_n\left(u_1u_2...u_{n-1}\right)>0\)
\(\Rightarrow u_{n+1}>u_n\Rightarrow\) dãy tăng
\(u_1=1;u_2=4=2^2;u_3=9=3^2\)
Dự đoán: \(u_n=n^2\)
- Với \(n=1;2;3\) dãy đúng
- Giả sử \(u_k=k^2\)
- Ta cần chứng minh \(u_{k+1}=\left(k+1\right)^2\)
Thật vậy, ta có:
\(u_{k+1}=u_k+2k+1=k^2+2k+1=\left(k+1\right)^2\) (đpcm)