

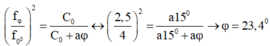
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


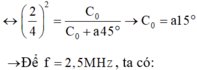
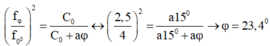

\(f=\frac{1}{2\pi\sqrt{LC}}\rightarrow C=\frac{1}{4\pi^2Lf^2}\) \(C=C_1+\frac{C_2-C_1}{120^o}\alpha\rightarrow120C\)\(=\left(120-\alpha\right)C_1+C_2\alpha\)
\(\rightarrow\frac{120}{f^2}=\frac{120-\alpha}{f^2_1}+\frac{\alpha}{f_2^2}\rightarrow\)\(\frac{120}{1,5^2}=\frac{120-\alpha}{3^2}+\frac{\alpha}{1^2}\rightarrow120.4=120-\alpha+9\alpha\)
\(\rightarrow8\alpha=360\rightarrow\alpha=45^o\)
Đáp án D

Tần số dao động riêng: \(f=\frac{1}{2\pi\sqrt{LC}}\Rightarrow\frac{1}{f^2}=k.C\)(Vì chỉ thay đổi C nên ta biểu diễn f theo C, k là một hệ số nào đó)
Suy ra:
\(\frac{1}{f_1^2}=k.C_1\)
\(\frac{1}{f_2^2}=k.C_2\)
Ta cần tìm:
\(\frac{1}{f^2}=k\left(C_1+C_2\right)\Rightarrow\frac{1}{f^2}=kC_1+kC_2\)
\(\Rightarrow\frac{1}{f^2}=\frac{1}{f_1^2}+\frac{1}{f_2^2}\)
Thay số ta đc f = 35Hz