Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Chọn gốc tọa độ tại đỉnh tháp, Oy hướng lên. Gốc thời gian là lúc ném vật.
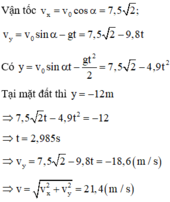

a)Qũy đạo của hòn đá: \(y=25+v_0sin\alpha\cdot t-\dfrac{1}{2}gt^2\)
Thời gian chuyển động của hòn đá:
\(\Rightarrow0=25+v_0\cdot sin\alpha\cdot t-\dfrac{1}{2}gt^2\)
\(\Rightarrow0=25+15\cdot sin30\cdot t-\dfrac{1}{2}\cdot10\cdot t^2\)
\(\Rightarrow t\approx3,11s\)
b)Khoảng cách từ chân tháp đến chỗ rơi:
\(S=x=v_0\cdot cos\alpha\cdot t\)
\(\Rightarrow S=15\cdot sin30\cdot3,11=23,325m\)
c)Ta có: \(v_x=v_0\cdot cos\alpha\)
\(v_y=v_0\cdot sin\alpha-gt\)
Vận tốc hòn đá lúc chạm đất:
\(v=\sqrt{(v_0\cdot sin\alpha)^2+\left(v_0\cdot sin\alpha-gt\right)^2}\)
\(=\sqrt{\left(15\cdot sin30\right)^2+\left(15\cdot sin30-10\cdot3,1\right)^2}\)
\(\approx24,7\)m/s
ở trên cho vx=v0⋅cosα sao xuống dưới chuyển thành sin rồi, v của bài này là 26,94 m/s ấy.

a)Phương trình quỹ đạo của hòn đá:
\(y=\dfrac{g}{2v^2_0}x^2\)
b)Thời gian chuyển động của hòn đá:
\(y=h=\dfrac{1}{2}gt^2\)
\(\Rightarrow t=\sqrt{\dfrac{2h}{g}}=\sqrt{\dfrac{2\cdot25}{10}}=\sqrt{5}\approx2,24s\)
c)Gọi gia tốc toàn phần là \(a=g=10\)m/s2
Gia tốc tiếp tuyến:
\(a_t=\dfrac{g\sqrt{2gh}}{\sqrt{v_0^2+2gh}}=\dfrac{10\sqrt{2\cdot10\cdot25}}{\sqrt{15^2+2\cdot10\cdot25}}=8,3\)m/s2
Gia tốc pháp tuyến:
\(a_n=\sqrt{a^2-a_t^2}=\sqrt{10^2-8,3^2}=5,6\)m/s2
Khoảng cách từ chân tháp đến lúc chạm đất:
\(R=\dfrac{v^2}{a_n}=\dfrac{15^2}{5,6}=40,18\)m

Hệ vật gồm hòn đá và Trái Đất. Chọn mặt đất làm gốc tính thế năng, chiều từ mặt đất lớn cao là chiều dương. Do chịu tác dụng của lực cản không khí, nên hệ vật ta xét không cô lập. Trong trường hợp này, độ biến thiên cơ năng của hệ vật có giá trị bằng công của lực cản.
W 2 - W 1 = (m v 2 /2 + mgz) - (m v 0 2 /2 + mgz0) = A c
Suy ra A c = m( v 2 - v 0 2 )/2 - mg z 0
Thay v 0 = 18 m/s, z 0 = 20 m, v = 20 m/s và z = 0, ta tìm được:
A c = 50. 10 - 3 /2( 20 2 - 18 2 ) - 50. 10 - 3 .10.20 = -8,1(J)

a. Chọn mốc Wt tại mặt đất.
Bỏ qua sức cản của không khí => cơ năng được bảo toàn.
Gọi vị trí ném vật là A
WtA=m.g.hA = 0,05.10.10 = 5 (J)
WđA=\(\dfrac{1}{2}\).m.vA2=\(\dfrac{1}{2}\).0,05.102=\(\dfrac{5}{2}\)(J)
b.Gọi vị trí vật chạm đất là B.
WB=WA= WtA + WđA = \(\dfrac{15}{2}\)(J)
Khi đó WtB = 0 (J)
=> WđB = \(\dfrac{15}{2}\)
=> \(\dfrac{1}{2}\).m.vB2 = \(\dfrac{1}{2}\).0,05.vB2=\(\dfrac{15}{2}\)
<=> vB = 10\(\sqrt{3}\)(m/s)
c. Gọi độ cao cực đại mà vật có thể đạt được so với mặt đất là C, khi đó vC=0 (m/s) <=> WđC=0
WC=WA=7,5=WtC
<=> m.g.hC=7,5
<=> 0,05.10.hC=7,5
<=> hC = 15 (m)
d. Gọi vị trí Wđ = 2Wt là D
Khi đó \(\dfrac{1}{2}\).m.vD2 = 2.m.g.hD
WD = WA = 7,5
=> \(\dfrac{1}{2}\).m.vD2 + m.g.hD = 7,5
<=> 3.m.g.hD = 7.5
<=> hD = 5(m)
Khi đó vD = 10\(\sqrt{2}\)(m/s) (Thay hD vào rồi tính được vD nhé)

a)
Chọn chiều (+) hướng lên. Gốc thời gian lúc bắt đầu ném
\(y=v_0t+\frac{gt2}{2}=20t-5t^2\) (1)
\(v=v_0+gt=20-10t\) (2)
Tại điểm cao nhất v=0
Từ (2) \(\Rightarrow\) t=2(s) thay vào (1)
yM = 20(m)
b)
Khi chạm đất y=0 từ (1)\(\Rightarrow\) t=0 và t=4 (s)
Thay t = 4 (s) vào (2) \(v'=-20m\text{/}s\)
(Dấu trừ (-) vận tốc ngược với chiều dương.)
Đáp án: D
Chọn gốc tọa độ tại đỉnh tháp, Oy hướng lên. Gốc thời gian là lúc ném vật.
Vận tốc:
Có:
Tại mặt đất thì :