Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
Tập hợp các chữ số chẵn chọn từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7 là {0,2,4,6}.
Tập hợp các chữ số lẻ chọn từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7 là {1,3,5,7}
+ Số các tự nhiên có 5 chữ số đôi một khác nhau thỏa đề có dạng
a
b
c
d
e
¯
(a có thể bằng 0), đồng thời ba chữ số chẵn đứng liền nhau, hai chữ số lẻ đứng liền nhau là ![]()
(để ý: có 2 cách xếp 3 chữ số chẵn thỏa đề {a,b,c}, {c,d,e})
+ Số các tự nhiên có 5 chữ số đôi một khác nhau thỏa đề có dạng
0
b
c
d
e
¯
, đồng thời ba chữ số chẵn đứng liền nhau, hai chữ số lẻ đứng liền nhau là ![]()
(để ý: có 1 cách xếp sao cho hai chữ số chẵn còn lại đứng liền với số 0 là {b,c}).
Suy ra, số các số tự nhiên thỏa đề ra là ![]()

Chọn B.
Tập hợp các chữ số chẵn chọn từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7 là {0,2,4,6}.
Tập hợp các chữ số lẻ chọn từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7 là {1,3,5,7}
+ Số các tự nhiên có 5 chữ số đôi một khác nhau sao cho có đúng 3 chữ số chẵn và 2 chữ số lẻ có dạng
a
b
c
d
e
¯
(a có thể bằng 0), đồng thời hai chữ số lẻ đứng liền nhau là ![]()
(để ý: có 4 cách xếp sao cho hai chữ số lẻ đứng liền nhau là ![]()
+ Số các số tự nhiên có 5 chữ số đôi một khác nhau sao cho có đúng 3 chữ số chẵn và 2 chữ số lẻ có dạng
0
b
c
d
e
¯
, đồng thời hai chữ số lẻ đứng liền nhau là ![]()
(để ý: có 3 cách xếp sao cho hai chữ số lẻ đứng liền nhau là ![]()
Suy ra, số các số tự nhiên thỏa đề ra là ![]()

Chọn C
Tập hợp các chữ số chẵn chọn từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7 là {0,2,4,6}.
Tập hợp các chữ số lẻ chọn từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7 là {1,3,5,7}
+ Số các số tự nhiên có 5 chữ số đôi một khác nhau thỏa đề có dạng
a
b
c
d
e
¯
(a có thể bằng 0), có đúng 3 chữ số chẵn và 2 chữ số lẻ, đồng thời ba chữ số chẵn và hai chữ số lẻ đứng xen kẽ là ![]()
(để ý: có 1 cách xếp 3 chữ số chẵn thỏa đề {a,c,e}).
+ Số các số tự nhiên có 5 chữ số đôi một khác nhau thỏa đề có dạng
0
b
c
d
e
¯
, có đúng 3 chữ số chẵn và 2 chữ số lẻ, đồng thời ba chữ số chẵn và hai chữ số lẻ đứng xen kẽ là ![]()
(để ý: có 1 cách xếp 3 chữ số chẵn thỏa đề {0,c,e}).
Suy ra, số các số tự nhiên thỏa đề ra là ![]()

Ta có 5 cách chọn hàng chục và bốn cách chọn hàng đơn vị nên ta có 4*5=20 số

Chọn A
Tập hợp các chữ số chẵn chọn từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7 là {0,2,4,6}.
Tập hợp các chữ số lẻ chọn từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7 là {1,3,5,7}.
Ta có,
+ Số các tự nhiên có 5 chữ số đôi một khác nhau sao cho có đúng 3 chữ số chẵn và 2 chữ số lẻ có dạng
a
b
c
d
e
¯
(a có thể bằng 0) là ![]() .
.
+ Số các tự nhiên có 5 chữ số đôi một khác nhau sao cho có đúng 3 chữ số chẵn và 2 chữ số lẻ có dạng
0
b
c
d
e
¯
là ![]()
Suy ra, số các số tự nhiên thỏa đề ra là ![]() .
.
Ý tưởng phát triển câu 39: thêm ràng buộc về thứ tự sắp xếp cho số tự nhiên lập được.

Đáp án là A.
Gọi số cần lập có dạng: a 1 a 2 a 3 a 4 a 5
• Chọn 2 số lẻ thuộc nhóm {1 ;3 ;5 ;7} ⇒ C 4 2
• Chọn 3 số chẳn trong nhóm {0;2;4;6} ⇒ C 4 3
• Hoán vị 2 nhóm trên có 5! cách
* Các số có số a1 = 0
• Chọn 2 số lẻ thuộc nhóm {1 ;3 ;5 ;7} ⇒ C 4 2
• Chọn 2 số chẳn trong nhóm {0;2;4;6} ⇒ C 3 2
• Hoán vị 2 nhóm trên có 4! cách
Vậy các số cần tìm: C 4 2 . C 4 3 . 5 ! - C 4 2 . C 3 2 . 4 ! = 2448 số

1. số tự nhiên có dạng abce ( nhớ gạch trê đầu ( vì đây là số tự nhiên))
* ta có h là :
h= mn
trong đó tập hợp mn là {0,1}
=> có 2 trường hợp xảy ra
(m,n)=(1,0) hoặc (0,1)
* ta có số tự nhiên abhe có tập hợp {h,2,3,4,5,6,7,8,9}
a có 9 cách chọn
b có 8 cách chọn
c có 7 cách chọn
e có 6 cách chọn
vậy có 9*8*7*6=3024 số
*ta phải loại trường hợp h đứng đầu và có dạng 01
trường hợp h đứng đầu và có dạng 01 có số cách chọn là :
a có 1 cách chọn là h
b có 8 cách
c có 7 cách
e có 6 cách
=> có 1*8*7*6=336 số
vậy số tự nhiên theo yêu cầu đề bài có tổng cộng
3024 - 332688 số
0 chắc

Không gian mẫu: \(n_{\Omega}=A_8^5-A_7^4=5880\)
Chọn 3 chữ số chẵn: \(C_4^3=4\) cách
Chọn 2 chữ số lẻ: \(C_4^2=6\) cách
Xếp 2 số lẻ liền nhau, sau đó hoán vị với 3 chữ số chẵn: \(2!.4!=48\) cách
Chọn 3 chữ số chẵn sao cho có mặt chữ số 0: \(C_3^2=3\) cách
Hoán vị 5 chữ số sao cho 2 số lẻ liền nhau và số 0 đứng đầu: \(2!.3!=12\) cách
\(\Rightarrow6.\left(4.48-3.12\right)=936\)
Xác suất: \(P=\dfrac{936}{5880}=\dfrac{39}{245}\)

Số tự nhiên chẵn gồm 5 chữ số khác nhau và đúng hai chữ số lẻ có:
· Chọn 2 chữ số lẻ có ![]() cach; chọn 3 chữ số chẵn có
cach; chọn 3 chữ số chẵn có ![]() cách
cách
· Gọi số có 5 chữ số thỏa mãn đề bài là ![]() .
.
· Nếu a5 = 0 thì có 4! Cách chọn ![]() .
.
· Nếu a5 ≠ 0 thì có 2 cách chọn a5 từ 3 số chẵn đã chọn; khi đó có 3 cách chọn a1 ; 3 cách chọn a2 ; 2 cách chọn a3 và 1 cách chọn a1 .
· Theo quy tắc cộng và nhân có 10.10.(1.4!+2.3.3.2.1)=6000 số
Số tự nhiên chẵn gồm 5 chữ số khác nhau và có đúng hai chữ số lẻ đứng cạnh nhau có ![]() số.
số.
Suy ra có 6000-3120=2880 số cần tìm.
Chọn D.
Chọn D
Tập hợp các chữ số chẵn chọn từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7 là {0,2,4,6}
Tập hợp các chữ số lẻ chọn từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7 là {1,3,5,7}
+ Số các số tự nhiên có 5 chữ số đôi một khác nhau sao cho có đúng 3 chữ số chẵn và 2 chữ số lẻ có dạng
a b c d e ¯ (a có thể bằng 0), đồng thời ba chữ số chẵn đứng liền nhau là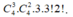
(để ý: có 3 cách xếp sao cho ba chữ số chẵn đứng liền nhau là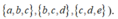
+ Số các tự nhiên có 5 chữ số đôi một khác nhau sao cho có đúng 3 chữ số chẵn và 2 chữ số lẻ có dạng 0 b c d e ¯ , đồng thời ba chữ số chẵn đứng liền nhau là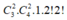
(để ý: có 1 cách xếp sao cho hai chữ số chẵn còn lại đứng liền với số 0 là {b;c})
Suy ra, số các số tự nhiên thỏa đề ra là