
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

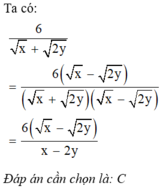

a: \(=6\cdot\sqrt{\dfrac{2xy}{4y^2}}\)
\(=6\cdot\dfrac{\sqrt{2xy}}{-2y}=-\dfrac{3\sqrt{2xy}}{y}\)
b: \(=\dfrac{4xy^2}{3}\cdot\dfrac{3}{\sqrt{xy}}=4\sqrt{x}\cdot y\sqrt{y}\)

a: \(=\dfrac{\left(1-\sqrt{2}\right)^2}{1-\sqrt{2}}=1-\sqrt{2}\)
b: \(=\dfrac{\sqrt{xy}\left(\sqrt{x}-\sqrt{y}\right)}{x-y}=\dfrac{\sqrt{xy}}{\sqrt{x}+\sqrt{y}}\)
d: \(=\dfrac{\left(\sqrt{x}-\sqrt{y}\right)\left(x+\sqrt{xy}+y\right)}{x-y}=\dfrac{x+\sqrt{xy}+y}{\sqrt{x}+\sqrt{y}}\)

\(x=\frac{2}{2\sqrt[3]{2}+2+\sqrt[3]{4}}=\frac{2\left(\sqrt[3]{4}-\sqrt[3]{2}\right)}{\left(\sqrt[3]{4}-\sqrt[3]{2}\right)\left(\sqrt[3]{4^2}+\sqrt[3]{4}.\sqrt[3]{2}+\sqrt[3]{2^2}\right)}\)
\(=\frac{2\left(\sqrt[3]{4}-\sqrt[3]{2}\right)}{\left(\sqrt[3]{4}\right)^3-\left(\sqrt[3]{2}\right)^3}=\sqrt[3]{4}-\sqrt[3]{2}\)
\(y=\frac{6}{2\sqrt[3]{2}-2+\sqrt[3]{4}}=\frac{2\left(\sqrt[3]{4}+\sqrt[3]{2}\right)}{\left(\sqrt[3]{4}+\sqrt[3]{2}\right)\left(\sqrt[3]{4^2}-\sqrt[3]{4}.\sqrt[3]{2}+\sqrt[3]{2^2}\right)}\)
\(=\frac{6\left(\sqrt[3]{4}+\sqrt[3]{2}\right)}{\left(\sqrt[3]{4}\right)^3+\left(\sqrt[3]{2}\right)^3}=\sqrt[3]{4}+\sqrt[3]{2}\)
\(P=\frac{xy}{x+y}=\frac{\sqrt[3]{4^2}-\sqrt[3]{2^2}}{2\sqrt[3]{4}}=\frac{\sqrt[3]{4}-1}{2}\)

\(a,\frac{2xy}{2\sqrt{x}+3\sqrt{y}}=\frac{2xy.\left(2\sqrt{x}-3\sqrt{y}\right)}{\left(2\sqrt{x}+3\sqrt{y}\right)\left(2\sqrt{x}-3\sqrt{y}\right)}=\frac{4x\sqrt{x}y-6xy\sqrt{y}}{2x-3y}\)
\(b,\frac{\sqrt{x}+\sqrt{y}}{2\sqrt{x}}=\frac{\left(\sqrt{x}+\sqrt{y}\right)\sqrt{x}}{2\sqrt{x}\sqrt{x}}=\frac{x+\sqrt{xy}}{2x}\)
\(c,\frac{2}{\sqrt{3}+1}=\frac{2\left(\sqrt{3}-1\right)}{\left(\sqrt{3}+1\right)\left(\sqrt{3}-1\right)}=\frac{2.\left(\sqrt{3}-1\right)}{2}=\sqrt{3}-1\)
\(d,\frac{6}{2\sqrt{3}+\sqrt{2}}=\frac{6\left(2\sqrt{3}-\sqrt{2}\right)}{\left(2\sqrt{3}+\sqrt{2}\right)\left(2\sqrt{3}-\sqrt{2}\right)}=\frac{6\left(2\sqrt{3}-\sqrt{2}\right)}{10}=\frac{6\sqrt{3}-3\sqrt{2}}{5}\)

\(a,\frac{1}{\sqrt{2}+\sqrt{3}-\sqrt{6}}=\frac{\sqrt{2}+\sqrt{3}+\sqrt{6}}{\left(\sqrt{2}+\sqrt{3}-\sqrt{6}\right)\left(\sqrt{2}+\sqrt{3}+\sqrt{6}\right)}=\frac{\sqrt{2}+\sqrt{3}+\sqrt{6}}{\left(\sqrt{2}+\sqrt{3}\right)^2-\sqrt{6}^2}\)
\(=\frac{\sqrt{2}+\sqrt{3}+\sqrt{6}}{2\sqrt{6}-1}=\frac{\left(\sqrt{2}+\sqrt{3}+\sqrt{6}\right)\left(2\sqrt{6}+1\right)}{2\sqrt{6}^2-1^2}=\frac{4\sqrt{3}+6\sqrt{2}+12+\sqrt{2}+\sqrt{3}+\sqrt{6}}{11}\)\(=\frac{\sqrt{6}+5\sqrt{3}+7\sqrt{2}+12}{11}\)
\(b,\frac{1}{\sqrt{x}+\sqrt{y}+\sqrt{z}}=\frac{\sqrt{x}+\sqrt{y}-\sqrt{z}}{\left(\sqrt{z}+\sqrt{y}+\sqrt{z}\right)\left(\sqrt{x}+\sqrt{y}-\sqrt{z}\right)}=\frac{\sqrt{x}+\sqrt{y}-\sqrt{z}}{\left(\sqrt{x}+\sqrt{y}\right)^2-\sqrt{z}^2}\)
\(=\frac{\sqrt{x}+\sqrt{y}-\sqrt{z}}{x+2\sqrt{xy}+y-z}\)

bài 2:
a: \(\dfrac{25}{5-2\sqrt{3}}=\dfrac{125+10\sqrt{3}}{13}\)
b: \(\dfrac{8}{\sqrt{5}+2}=8\sqrt{5}-32\)
c: \(\dfrac{6}{2\sqrt{3}-\sqrt{7}}=\dfrac{12\sqrt{3}+6\sqrt{7}}{5}\)
d: \(=\dfrac{\sqrt{3}\left(3\sqrt{3}-2\right)}{\sqrt{2}\left(3\sqrt{3}-2\right)}=\dfrac{\sqrt{6}}{2}\)

\(a,\frac{\sqrt{108x^3}}{\sqrt{12x}}=\frac{\sqrt{36.3.x^3}}{\sqrt{3.4.x}}=\frac{6\sqrt{3}.\sqrt{x}^3}{2\sqrt{3}.\sqrt{x}}=3\sqrt{x}^2=3x\)
\(b,\frac{\sqrt{13x^4y^6}}{\sqrt{208x^6y^6}}=\frac{\sqrt{13}.\sqrt{x^4}.\sqrt{y^6}}{\sqrt{16.13}.\sqrt{x^6}.\sqrt{y^6}}=\frac{\sqrt{13}.x^2y^3}{4\sqrt{13}x^3y^3}=\frac{1}{4x}\)
\(c,\frac{x\sqrt{x}+y\sqrt{y}}{\sqrt{x}+\sqrt{y}}-\left(\sqrt{x}+\sqrt{y}\right)^2\)
\(=\frac{\sqrt{x}^3+\sqrt{y}^3}{\sqrt{x}+\sqrt{y}}-\left(x+2\sqrt{xy}+y\right)\)
\(=\frac{\left(\sqrt{x}+\sqrt{y}\right)\left(x-\sqrt{xy}+y\right)}{\sqrt{x}+\sqrt{y}}-x-2\sqrt{xy}-y\)
\(=x-\sqrt{xy}+y-x-2\sqrt{xy}-y=-3\sqrt{xy}\)
\(d,\sqrt{\frac{x-2\sqrt{x}+1}{x+2\sqrt{x}+1}}=\frac{\sqrt{\left(\sqrt{x}-1\right)^2}}{\sqrt{\left(\sqrt{x}+1\right)^2}}=\frac{\sqrt{x}-1}{\sqrt{x}+1}\)
Đk chỗ này là \(\sqrt{x}-1\ge0\Rightarrow\sqrt{x}\ge\sqrt{1}\Rightarrow x\ge1\)nhé
\(e,\frac{x-1}{\sqrt{y}-1}.\sqrt{\frac{\left(y-2\sqrt{y}+1\right)^2}{\left(x-1\right)^4}}=\frac{x-1}{\sqrt{y}-1}.\frac{y-2\sqrt{y}+1}{\left(x-1\right)^2}\)
\(=\frac{\left(x-1\right)\left(\sqrt{y}-1\right)^2}{\left(\sqrt{y}-1\right)\left(x-1\right)^2}=\frac{\sqrt{y}-1}{x-1}\)