Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1:
\(\overrightarrow{MN}=\left(3;-1;-4\right)\Rightarrow\) pt mặt phẳng trung trực của MN:
\(3\left(x-\frac{7}{2}\right)-\left(y-\frac{1}{2}\right)-4\left(z-2\right)=0\Leftrightarrow3x-y-4z-2=0\)
\(\overrightarrow{PN}=\left(4;3;-1\right)\Rightarrow\) pt mp trung trực PN: \(4x+3y-z-7=0\)
\(\Rightarrow\) Phương trình đường thẳng giao tuyến của 2 mp trên: \(\left\{{}\begin{matrix}x=1+t\\y=1-t\\z=t\end{matrix}\right.\)
\(\Rightarrow I\left(1+c;1-c;c\right)\) \(\Rightarrow\overrightarrow{NI}=\left(c-4;1-c;c\right)\)
\(d\left(I;\left(Oyz\right)\right)=IN\Rightarrow\left|1+c\right|=\sqrt{\left(c-4\right)^2+\left(1-c\right)^2+c^2}\)
\(\Leftrightarrow\left(c+1\right)^2=3c^2-10c+17\)
\(\Leftrightarrow2c^2-12c+16=0\Rightarrow\left[{}\begin{matrix}c=4\\c=2\end{matrix}\right.\)
Mà \(a+b+c< 5\Rightarrow\left(1+c\right)+\left(1-c\right)+c< 5\Rightarrow c< 3\Rightarrow c=2\)
Câu 2:
Phương trình tham số d: \(\left\{{}\begin{matrix}x=-1+2t\\y=t\\z=2-t\end{matrix}\right.\) \(\Rightarrow C\left(-1+2n;n;2-n\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AC}=\left(2n;n-3;1-n\right)\\\overrightarrow{AB}=\left(1;-1;-2\right)\end{matrix}\right.\) \(\Rightarrow\left[\overrightarrow{AB};\overrightarrow{AC}\right]=\left(3n-7;-3n-1;3n-3\right)\)
\(\Rightarrow S_{ABC}=\frac{1}{2}\left|\left[\overrightarrow{AB};\overrightarrow{AC}\right]\right|=2\sqrt{2}\)
\(\Leftrightarrow\sqrt{\left(3n-7\right)^2+\left(-3n-1\right)^2+\left(3n-3\right)^2}=4\sqrt{2}\)
\(\Leftrightarrow27n^2-54n+27=0\Rightarrow n=1\)
\(\Rightarrow C\left(1;1;1\right)\Rightarrow m+n+p=3\)

B C A D H K J S
Kẻ \(SH\perp AC\left(H\in AC\right)\)
Do \(\left(SAC\right)\perp\left(ABCD\right)\Rightarrow SH\perp\left(ABCD\right)\)
\(SA=\sqrt{AC^2-SC^2}=a;SH=\frac{SA.SC}{AC}=\frac{a\sqrt{3}}{2}\)
\(S_{ABCD}=\frac{AC.BD}{2}=2a^2\)
\(V_{S.ABCD}=\frac{1}{3}SH.S_{ABCD}=\frac{1}{3}.\frac{a\sqrt{3}}{2}.2a^2=\frac{a^3\sqrt{3}}{3}\)
Ta có \(AH=\sqrt{SA^2-SH^2}=\frac{a}{2}\Rightarrow CA=4HA\Rightarrow d\left(C,\left(SAD\right)\right)=4d\left(H,\left(SAD\right)\right)\)
Do BC//\(\left(SAD\right)\Rightarrow d\left(B,\left(SAD\right)\right)=d\left(C,\left(SAD\right)\right)=4d\left(H,\left(SAD\right)\right)\)
Kẻ \(HK\perp AD\left(K\in AD\right),HJ\perp SK\left(J\in SK\right)\)
Chứng minh được \(\left(SHK\right)\perp\left(SAD\right)\) mà \(HJ\perp SK\Rightarrow HJ\perp\left(SAD\right)\Rightarrow d\left(H,\left(SAD\right)\right)=HJ\)
Tam giác AHK vuông cân tại K\(\Rightarrow HK=AH\sin45^0=\frac{a\sqrt{2}}{4}\)
\(\Rightarrow HJ=\frac{SH.HK}{\sqrt{SH^2+HK^2}}=\frac{a\sqrt{3}}{2\sqrt{7}}\)
Vậy \(d\left(B,\left(SAD\right)\right)=\frac{2a\sqrt{3}}{\sqrt{7}}=\frac{2a\sqrt{21}}{7}\)

14.
Mặt phẳng (P) nhận \(\overrightarrow{n}=\left(2;1;-2\right)\) là 1 vtpt
Đường thẳng d nhận \(\overrightarrow{u}=\left(1;-2;3\right)\) là 1 vtcp
Điểm \(M\left(2;0;-3\right)\) thuộc d nên cũng thuộc (Q)
(Q) vuông góc (P) và chứa d nên nhận \(\left[\overrightarrow{n};\overrightarrow{u}\right]=\left(1;8;5\right)\) là 1 vtpt
Phương trình (Q):
\(1\left(x-2\right)+8y+5\left(z+3\right)=0\)
\(\Leftrightarrow x+8y+5z+13=0\)
15.
Phương trình hoành độ giao điểm:
\(sinx=cosx\Rightarrow x=\frac{\pi}{4}\)
\(S=\int\limits^{\frac{\pi}{4}}_0\left(cosx-sinx\right)dx+\int\limits^{\pi}_{\frac{\pi}{4}}\left(sinx-cosx\right)dx=\sqrt{2}-1+\sqrt{2}+1=2\sqrt{2}\)
10.
Coi lại đề nào bạn, pt hình phẳng (D) có vấn đề, nhìn chữ -dx+4 kia ko biết phải nghĩ sao
11.
Cũng ko dịch được đề này, đoán đại: cho \(F\left(x\right)=x^2\) là 1 nguyên hàm của \(f\left(x\right).e^{2x}\). Tìm nguyên hàm của \(f'\left(x\right).e^{2x}\)
\(I=\int f'\left(x\right)e^{2x}dx\)
Đặt \(\left\{{}\begin{matrix}u=e^{2x}\\dv=f'\left(x\right)dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=2e^{2x}dx\\v=f\left(x\right)\end{matrix}\right.\)
\(\Rightarrow I=e^{2x}f\left(x\right)-2\int f\left(x\right)e^{2x}dx=e^{2x}f\left(x\right)-2x^2+C\)
12.
Đúng là \(y=\left(e+1\right)x\) và \(y=1+e^x\) chứ bạn? Hai đồ thị này cắt nhau tại 2 điểm, nhưng ko thể tìm được tọa độ của điểm thứ 2 đâu
13.
Hình chiếu của A lên Ox có tọa độ \(\left(1;0;0\right)\)

Gọi pt mặt phẳng (Q) song song (P) có dạng \(x+2y-2z+d=0\)
Lấy \(A\left(-3;0;0\right)\) là một điểm thuộc (P)
\(d\left(A;\left(Q\right)\right)=\frac{\left|-3+d\right|}{\sqrt{1^2+2^2+2^2}}=\frac{\left|d-3\right|}{3}=2\Rightarrow\left[{}\begin{matrix}d=9\\d=-3\end{matrix}\right.\)
\(\Rightarrow\) Phương trình (Q): \(\left[{}\begin{matrix}x+2y-2z+9=0\\x+2y-2z-3=0\end{matrix}\right.\)
Bạn tìm giao điểm của d và (Q) sẽ ra tọa độ điểm M
Nhưng thi trắc nghiệm thì lẹ nhất là thay thẳng 4 đáp án vào kiểm tra

Câu 28:
\(\overrightarrow{CB}=\left(1;-1;1\right)\)
Do (P) vuông góc BC nên nhận (1;-1;1) là 1 vtpt
Phương trình (P):
\(1\left(x-1\right)-1\left(y-1\right)+1\left(z+5\right)=0\)
\(\Leftrightarrow x-y+z+5=0\)
Câu 29:
Mạt phẳng (Q) nhận \(\left(1;-2;3\right)\) là 1 vtpt nên nhận các vecto có dạng \(\left(k;-2k;3k\right)\) cũng là các vtpt với \(k\ne0\)
Do đó đáp án B đúng (ko tồn tại k thỏa mãn)
Với đáp án A thì \(k=-2\) , đáp án C thì \(k=3\), đáp án D có \(k=1\)

a) Gọi \(\overrightarrow{u}\left(1;-2;-1\right)\) là vectơ chỉ phương của d, giả sử \(\overrightarrow{v}\left(a;b;c\right)\) là 

Chọn A
Cách 1: Ta có: B ∈ Oxy và B ∈ (α) nên B (a ; 2 – 2a ; 0).
Ta có: d ⊂ (α) nên d và Δ song song với nhau và cùng nằm trong mặt phẳng (α).
Gọi C = d ∩ (Oxy) nên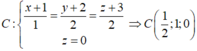
Gọi d’ = (α) ∩ (Oxy), suy ra d’ thỏa hệ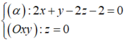
Do đó, d’ qua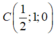 và có VTCP
và có VTCP 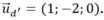
Gọi φ = (Δ, d’) = (d, d’)
Gọi H là hình chiếu của C lên Δ. Ta có CH = 3 và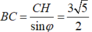
Cách 2: Ta có: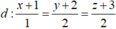 đi qua M (-1 ; -2 ; -3) và có một VTCP là
đi qua M (-1 ; -2 ; -3) và có một VTCP là 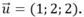
Ta có: B = Δ ∩ (Oxy), Δ ⊂ (α) nên B ∈ (Oxy) ∩ (α) => B (a; 2 – a; 0)
Ta có: Δ // d và d (Δ, d) = 3 nên