Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn đáp án A
Ta có λ 1 : λ 2 : λ 3 = 0 , 38 : 0 , 57 : 0 , 76 = 2 : 3 : 4 → BCNN là 12
→ Trong khoảng giữa hai vân sáng trùng màu với vân sáng trung tâm có:
- 5 vân sáng λ 1 ; 3 vân sáng λ 2 , 2 vân sáng λ 3 .
- BCNN λ 1 , λ 2 là 6 → có 1 vân trùng đôi của λ 1 , λ 2
- BCNN λ 1 , λ 3 là 4 → có 2 vân trùng đôi của λ 1 , λ 3
- BCNN λ 2 , λ 3 là 12 → không có vân trùng đôi của λ 2 , λ 3
→ Trong khoảng giữa hai vân sáng trùng màu với vân sáng trung tâm có 5 + 3 + 2 – 2(1 + 2 + 0) = 4 vân sáng đơn sắc.
Đáp án B
Ta có:
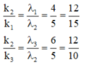
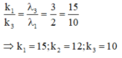
Xét trong khoảng giữa vị trí vân sáng trung tâm có k1=0 , k2=0, k3=0 và vân sáng gần nhất cùng màu với vân sáng trung tâm có k1=15, k2=12, k3=10
Các vị trí trùng nhau của VS1 và VS2 là: (k1;k2)=(4;5),(8;10)
Các vị trí trùng nhau của VS2 và VS3 là: (k2,k3)=(6;5)
Các vị trí trùng nhau của VS1 và VS3 là: 
=> Số vị trí mà ở đó chỉ có một bức xạ cho vân sáng là:
Đáp án B
Vị trí trùng màu với vân trung tâm là vị trí trùng nhau của vân sáng 3 bức xạ :
→ Vị trí trùng nhau gần vân trung tâm nhất ứng với k1 = 15, k2 = 12 và k3 = 10
+ Sự trùng nhau của hai bức xạ λ1 và λ2 trong khoảng này
→
có 2 vị trí trùng nhau của hai hệ vân ứng với k1 = 5, 10
+ Sự trùng nhau của hai bức xạ λ1 và λ3 trong khoảng này :
→
có 4 vị trí trùng nhau của hai hệ vân ứng với k1 = 3, 6, 9 và 12
+ Sự trùng nhau của hai bức xạ λ2 và λ3 trong khoảng này :
→
có 1 vị trí trùng nhau của hai hệ vân ứng với k2 = 6
Vậy số vị trí cho vân đơn sắc là 14 + 11 + 9 – 2.2 – 2.4 – 2.1 = 20
Phương pháp:
Áp dụng điều kiện trùng nhau của các vân sáng trong giao thoa sóng ánh sáng
Cách giải: Đáp án B
Vị trí trùng màu với vân trung tâm là vị trí trùng nhau của vân sáng 3 bức xạ : x1 = x2 = x3
=> 4k1 = 5k2 = 6k3
→ Vị trí trùng nhau gần vân trung tâm nhất ứng với k1 = 15, k2 = 12 và k3 = 10
+ Sự trùng nhau của hai bức xạ λ1 và λ2 trong khoảng này
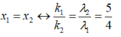
→ có 2 vị trí trùng nhau của hai hệ vân ứng với k1 = 5, 10
+ Sự trùng nhau của hai bức xạ λ1 và λ3 trong khoảng này:
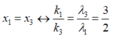
→ có 4 vị trí trùng nhau của hai hệ vân ứng với k1 = 3, 6, 9 và 12
+ Sự trùng nhau của hai bức xạ λ2 và λ3 trong khoảng này :
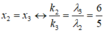
→ có 1 vị trí trùng nhau của hai hệ vân ứng với k2 = 6
Vậy số vị trí cho vân đơn sắc là 14 + 11 + 9 – 2.2 – 2.4 – 2.1 = 20
Đáp án: A
+ Điều kiện vân sáng của λ1 trùng với vân sáng của λ2:
k2/k1 = λ1/λ2 = 0,42/0,56 = a/b = 3/4
+) Điều kiện vân sáng của λ1 trùng với vân sáng của λ3:
k3/k1 = λ1/λ3 = 0,42/0,63 = c/d = 2/3
+) Điều kiện vân sáng của λ2 trùng với vân sáng của λ3:
k3/k2 = λ2/λ3 = 0,56/0,63 = e/f = 8/9
→ Khoảng vân trùng i = b.d.λ1 = a.d.λ2 = b.c.λ3
hay i = 12λ1 = 9λ2 = 8λ3
Trong khoảng giữa hai vân sáng liên tiếp có màu giống màu vân trung tâm, có 2 vị trí vân sáng bức xạ 1 trùng với bức xạ 2, 3 vị trí vân sáng bức xạ 1 trùng với bức xạ 3.
=> Số vân sáng quan sát được là N = (12 – 1)+ (9 – 1) + (8 – 1) – (2 + 3) = 21 vân
(2 vân sáng trùng nhau tính là 1)
Khoảng vân ứng với bước sóng \(\lambda\) là:
\(i=\lambda\frac{D}{d}=k\lambda\) (với \(k=\frac{D}{d}\))
Vân sáng trung tâm là cực đại chung của cả 3 bước sóng.
Cực đại chung gần nhất ứng với khoảng cách là bội chung nhỏ nhất của 3 khoảng vân.
Để đơn giản, ta tìm bội chung nhỏ nhất của 42, 56, 63. Mình sẽ hướng dẫn luôn.
Trước hết phân tích thành tích các số nguyên tố:
\(\text{42=7×2×3 }\)
\(56=7\text{×}2^3\)
\(63=7\text{×}3^2\)
Bội chung nhỏ nhất là: \(7\text{×}2^3\text{×}3^2=504\)
Vậy khoảng giữa 2 vân sáng liên tiếp có màu giống màu vân trung tâm là:\(d=5,04k\left(m\right)\)
Bội chung nhỏ nhất giữa 42 và 56 là: \(\text{7×}2^3\text{×}3=168\)
Suy ra trong khoảng \(d\) có 2 vân sáng là : \(\lambda_1\) và \(\lambda_2\) trùng nhau
Bội chung nhỏ nhất giữa 42 và 63 là: \(7\text{×}2\text{×}3^2=126\)
Suy ra trong khoảng \(d\)có 3 vân sáng là \(\lambda_1\) và \(\lambda_3\) trùng nhau.
Bội chung nhỏ nhất giữa 56 và 63 là: \(7\text{×}2^3\text{×}3^2=504\)
Suy ra trong khoảng \(d\) có 0 vân sáng là \(\lambda_2\) và \(\lambda_3\) trùng nhau.
Vậy tổng số vân sáng bên trong khoảng d là:
\(\frac{d}{i_1}-1+\frac{d}{i_2}-1+\frac{d}{i_3}-1-2-3-0\)
\(=\frac{504}{42}-1+\frac{504}{56}-1+\frac{504}{63}-1-2-3-0\)
\(=21\) (vân sáng )
----> chọn A
ta có:
\(i_1:i_2:i_3=\lambda_1:\lambda_2:\lambda_3=6:8:9\)
Bội chung nhỏ nhất là 72
Như vậy vân 12 của bức xạ 1 trùng với 9 của bx2 và 8 của bx3
trong khoảng này thì bx2 và và bx3 không trùng cực đại vì 8 và 9 nguyên tố cùng nhau
cực đại số 4 và số 8 của bx1 trùng với cực đại số 3 và 6 của bx2
cực đại số 3 ,6 và số 9 của bx1 trùng với cực đại số 2; 4và 6 của bx2
Số cực đại nhìn thấy là
11+8+7-2-3=21
\(\rightarrow chọn.A\)
Nguyên hóa \(\left(\lambda_1;\lambda_2;\lambda_3\right)=\left(4;5;6\right)\)
\(BCNN\left(4;5;6\right)=60\Rightarrow Bac:\left\{{}\begin{matrix}\lambda_1:\dfrac{60}{4}=15\\\lambda_2:\dfrac{60}{5}=12\\\lambda_3:\dfrac{60}{6}=10\end{matrix}\right.\)
\(\Rightarrow i_{trung}=15.i_1=\dfrac{15.\lambda_1.D}{a}\)
Có nghĩa là tìm số vân sáng tạo bởi 1 bức xạ trong khoảng
\(0< ...< \dfrac{15.\lambda_1.D}{a}\)
Ta nhận thấy bậc của bức xạ 1 tại vị trí trùng nhau của 3 bức xạ lần đầu tiên là bậc 15=> trong khoảng đang xét có 14 vân sáng của bức xạ 1
Tương tự, có 11 vân sáng của bx 2 và 9 vân sáng của bx 3
=>Tổng cộng có: \(14+11+9=34\left(van-sang\right)\)
Ta xét xem có những cặp bức xạ nào cho vân sáng trùng nhau
Xét bức xạ 1 và 2: \(\dfrac{k_1}{k_2}=\dfrac{\lambda_2}{\lambda_1}=\dfrac{5}{4}\Rightarrow i_{12}=5.i_1=\dfrac{5.\lambda_1.D}{a}\)
\(\Rightarrow So-van-trung=k_{12}.i_{12}=\dfrac{k_{12}.5.\lambda_1D}{a}\)
\(\Rightarrow0< \dfrac{5.k_{12}.\lambda_1.D}{a}< \dfrac{15.\lambda_1.D}{a}\Leftrightarrow0< k_{12}< 3\)
\(\Rightarrow k_{12}=1;2\)=> co 2 van trung cua buc xa 1 va buc xa 2
Xet bx 2 va bx 3 \(\dfrac{k_2}{k_3}=\dfrac{\lambda_3}{\lambda_2}=\dfrac{6}{5}\Rightarrow i_{23}=6.i_2=\dfrac{6.\lambda_2.D}{a}\)
\(\Rightarrow So-van-trung=k_{23}.i_{23}=\dfrac{k_{23}.6.\lambda_2.D}{a}\)
\(0< \dfrac{6k_{23}.\lambda_2.D}{a}< \dfrac{15.\lambda_1.D}{a}\Leftrightarrow0< k_{23}< 2\Rightarrow k_{23}=1\)
=> co 1 van trung cua bx 2 va bx 3
Xet bx 1 va bx 3 \(\dfrac{k_1}{k_3}=\dfrac{\lambda_3}{\lambda_1}=\dfrac{3}{2}\Rightarrow i_{13}=3.i_1=\dfrac{3.\lambda_1.D}{a}\)
\(\Rightarrow So-van-trung=k_{13}.i_{13}=\dfrac{k_{13}.3.\lambda_1.D}{a}\)
\(\Rightarrow0< \dfrac{3.k_{13}.\lambda_1.D}{a}< \dfrac{15.\lambda_1.D}{a}\Leftrightarrow0< k_{13}< 5\)
\(\Rightarrow k_{13}=1;2;3;4\)
=> co 4 van trung cua bx 1 va bx 3
\(\Rightarrow So-van-trung-tong-cong:4+2+1=7\left(van-trung\right)\)
Vậy số vân chỉ có 1 bức xạ cho vân sáng là: \(34-7=27\left(van\right)\)
Giữa hai vân sáng gần nhau nhất cùng màu với vân trung tâm có 8 vân sáng màu lục tức là khoảng cách đó là \(\Delta x _{min}= 9i_{lục}.\)
=> \(9i_{lục}= k_2 i_{đỏ}=> 9\lambda_{lục}= k_2 \lambda_{đỏ}\)
=> \(\lambda_{lục} = \frac{k_2 \lambda_{đỏ}}{9}.\ \ (1)\)
Mà \(500 n m \leq \lambda_{lục} \leq 575nm.\)
Thay (1) vào <=> \(500 n m \leq \frac{k_2 \lambda_{đỏ}}{9} \leq 575nm.\)
<=> \(\frac{500.9}{720} \leq k_2 \leq \frac{575.9}{720}\)
<=> \(6,25 \leq k_2 \leq 7,1875\)
=> \(k_2 = 7=> (1): \lambda_{lục} = 560nm.\)
720nm = 0,72 μm
giữa 2 vân sáng gần nhau nhất và cùng màu vs vân sáng trung tâm có 8 vân sáng màu lục => Tại vị trí trùng đó là VS bậc 9 của λlục
Tại VT trùng nhau: x_kđỏ = x_9lục
<=> kđỏ.λđỏ = 9.λlục
<=> kđỏ/9 = λlục/λđỏ = λ/0,72
=> λ = (0,72.kđỏ)/9 = 0,08.kđỏ (*)
0,5 ≤ λ = 0,08.kđỏ ≤ 0,575 μm
6,25 ≤ kđỏ ≤ 7,1875
=> kđỏ = 7
thế vào (*) λ = 0,56 (μm) = 560nm
đáp án : D
→ Trong khoảng giữa hai vân sáng trùng màu với vân sáng trung tâm có 5 + 3 + 2 – 2(1 + 2 + 0) = 4 vân sáng đơn sắc.
Đáp án C