Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tóm tắt:
\(a=10^{-3}m\)
\(D=0,5m\)
\(\lambda_1=0,64\mu m\)
\(\lambda_2=0,6\mu m\)
\(\lambda_3=0,54\mu m\)
\(\lambda_4=0,48\mu m\)
\(\Delta x=?\)
Giải:
Khi vân sáng trùng nhau:
\(k_1\lambda_1=\)\(k_2\lambda_2=\)\(k_3\lambda_3=\)\(k_4\lambda_4\) \(\Leftrightarrow k_10,64\)\(=k_20,6\)\(=\)\(k_30,54\)\(=k_40,48\)
\(\Leftrightarrow\)\(k_164=k_260=k_354=k_448\) \(\Leftrightarrow\) \(k_164=k_260=k_354=k_448\)
\(\Leftrightarrow k_132=k_230=k_327=k_424\)
BSCNN( 32;30;27;24 ) = 4320
\(k_1=\frac{4320}{32}=135\)
\(k_2=\frac{4320}{30}=144\)
\(k_3=\frac{4320}{27}=160\)
\(k_4=\frac{4320}{24}=180\)
Vậy \(\Delta x=135i_1=144i_2=160i_3=180i_4\)\(=0,0432m=4,32cm\)
\(\rightarrow D\)

Ta có \(\dfrac{i_1}{i_2}=\dfrac{4}{5}\)
Nên chọn \(\begin{cases}i_1=4i \\ i_2=5i \end{cases}\) \(\Rightarrow i_{\equiv }=20i\)
Tại vị trí \(x_1= 0,5i_1=2i; x_2=12,5i_1=50i\)
Nên số vân trùng thỏa mãn: \(2i < k.20i < 50i\)
Có 2 giá trị k thỏa mãn là: k = 1 hoặc k = 2.
Vậy có 2 vân trùng,
Chọn đáp án B.

Khi các vân sáng trùng nhau: \(k_1\lambda_1=k_2\lambda_2=k_3\lambda_3\)
k10,4 = k20,5 = k30,6 \(\Leftrightarrow\) 4k1 = 5k2 = 6k3
BSCNN(4,5,6) = 60
\(\Rightarrow\) k1 = 15 ; k2 = 12 ; k3 = 10 Bậc 15 của \(\lambda_1\) trùng bậc 12 của \(\lambda_2\) trùng với bậc 10 của \(\lambda_3\)
Trong khoảng giữa phải có: Tổng số VS tính toán = 14 + 11 + 9 = 34
Ta xẽ lập tỉ số cho tới khi k1 = 15 ; k2 = 12 ; k3 = 10
- Với cặp \(\lambda_1;\lambda_2:\) \(\frac{k_1}{k_2}=\frac{\lambda_1}{\lambda_2}=\frac{5}{4}=\frac{10}{8}=\frac{15}{12}\)
Như vậy: Trên đoạn từ vân VSTT đến k1 = 15 ; k2 = 12 thì có tất cả 4 vị trí trùng nhau
Vị trí 1: VSTT
Vị trí 2: k1 = 5 ; k2 = 4
Vị trí 3: k1 = 10 ; k2 = 8 => Trong khoảng giữa có 2 vị trí trùng nhau.
Vị trí 4: k1 = 15 ; k2 = 12
- Với cặp\(\lambda_2;\lambda_3:\) \(\frac{k_2}{k_3}=\frac{\lambda_3}{\lambda_2}=\frac{6}{5}=\frac{12}{10}\)
Như vậy: Trên đoạn từ vân VSTT đến k2 = 12 ; k3 = 10 thì có tất cả 3 vị trí trùng nhau
Vị trí 1: VSTT
Vị trí 2: k2 = 6 ; k3 = 5 \(\Rightarrow\) Trong khoảng giữa có 1 vị trí trùng nhau.
Vị trí 3: k2 = 12 ; k3 = 10
- Với cặp \(\lambda_1;\lambda_3:\) \(\frac{k_1}{k_3}=\frac{\lambda_3}{\lambda_1}=\frac{3}{2}=\frac{6}{4}=\frac{9}{6}=\frac{12}{8}=\frac{15}{10}\)
Như vậy: Trên đoạn từ vân VSTT đến k1 = 15 ; k3 = 10 thì có tất cả 6 vị trí trùng nhau
Vị trí 1: VSTT
Vị trí 2: k1 = 3 ; k3 = 2
Vị trí 3: k1 = 6 ; k3 = 4
Vị trí 4: k1 = 9 ; k3 = 6 \(\Rightarrow\) Trong khoảng giữa có 4 vị trí trùng nhau.
Vị trí 5: k1 = 12 ; k3 = 8
Vị trí 6: k1 = 15 ; k3 = 10
Vậy tất cả có 2 + 1 +4 = 7 vị trí trùng nhau của các bức xạ.
Số VS quan sát được = Tổng số VS tính toán – Số vị trí trùng nhau = 34 – 7 = 27 vân sáng.
\(\rightarrow D\)

Đáp án B
+ Khi sử dụng ánh sáng đơn sắc λ 1 và λ 2 , ta thấy giữa hai vân sáng gần nhau nhất cùng màu với vân trung tâm có 6 vân sáng ứng với λ 2 → Nếu ta xét vân đầu tiên trùng giữa hai hệ vân vân trung tâm thì vân thứ hai trùng nhau của hai hệ vân của bức xạ λ 2 ứng với k = 7.
→ Áp dụng điều kiện cho vân sáng trùng nhau của λ 1 và λ 2 → k 1 λ 1 = 7 λ 2 → λ 2 = k 1 . 0 , 56 7 = 0 , 08 k 1 .
+ Dựa vào khoảng giá trị của λ 2 là 0,65 μm < λ 2 < 0,75 μm → λ 2 = 0,72 μm.
+ Khi sử dụng ánh áng thì nghiệm gồm ba bức xạ đơn sắc, trong đó λ 3 = 2 3 λ 2 = 0 , 48 μm.
→ Áp dụng điều kiện trùng nhau của ba hệ vân k 1 λ 1 = k 2 λ 2 = k 3 λ 3 ↔ 7 k 1 = 9 λ 2 = 6 k 3
→ Tại vị trí trùng nhau của ba hệ vân sáng gần vân trung tâm nhất thì
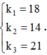
+ Điều kiện trùng nhau của vân sáng của hai bức xạ λ 1 và λ 2 là
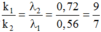
→ Giữa vân trung tâm và vân trùng màu gần vân trung tâm nhất có 1 vị trí trùng giữa vân sáng của λ 1 và λ 2 .
+ Điều kiện trùng nhau của vân sáng của hai bức xạ λ 3 và λ 2 là
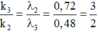
k 3 = 3, 6, 9, 12, 15, 18, 21
k 2 = 2, 4, 6, 8, 10, 12, 14
→ Giữa vân trung tâm và vân trùng màu gần vân trung tâm nhất có 6 vị trí trùng giữa vân sáng của λ 3 và λ 2 .
→ Giữa vân trung tâm và gân trùng màu gần nhất với vân trung tâm có 6 vân sáng đỏ

\(\lambda_1\)(tím)\(=0,42\mu m\) , \(\lambda_2\) (lục) \(=0,56\mu m\) , \(\lambda_3\) (đỏ) \(=0,7\mu m\)
Vì giữa hai vân sáng liên tiếp có màu giống như màu vân sáng trung tâm có 11 cực đại giao thoa của ánh sáng đỏ \(\Rightarrow k_{đỏ}=k_3=12\)
Từ BSCNN \(\Rightarrow k_1=k_{tím}=20\Rightarrow\) giữa hai vân sáng liên tiếp có màu giống như màu vân sáng trung tâm có 19 vân màu tím
\(\Rightarrow k_{lục}=k_2=15\Rightarrow\) giữa hai vân sáng liên tiếp có màu giống như màu vân sáng trung tâm có 14 vân màu lục.
\(\rightarrow A\)

Tóm tắt:
a = \(10^{-3}m\)
D = \(1,25m\)
\(\lambda_1=0,64\mu m\)
\(\lambda_2=0,48\mu m\)
\(\Delta x=?\)
Giải:
Khi vân sáng trùng nhau:
\(k_1\lambda_1=k_2\lambda_2\Rightarrow\)\(\frac{k_1}{k_2}=\frac{\lambda_2}{\lambda_1}=\frac{0,48}{0,64}=\frac{3}{4}\)
Vậy: \(k_1=3;k_2=4\)\(\Rightarrow\Delta x=3i_1=3.\frac{\lambda_1.D}{a}=3.\)\(\frac{0,64.10^{-6}.1,25}{10^{-3}}=2,4.10^{-3}m=2,4mm\)
\(\rightarrow D\)

Giữa hai vân sáng gần nhau nhất cùng màu với vân trung tâm có 8 vân sáng màu lục tức là khoảng cách đó là \(\Delta x _{min}= 9i_{lục}.\)
=> \(9i_{lục}= k_2 i_{đỏ}=> 9\lambda_{lục}= k_2 \lambda_{đỏ}\)
=> \(\lambda_{lục} = \frac{k_2 \lambda_{đỏ}}{9}.\ \ (1)\)
Mà \(500 n m \leq \lambda_{lục} \leq 575nm.\)
Thay (1) vào <=> \(500 n m \leq \frac{k_2 \lambda_{đỏ}}{9} \leq 575nm.\)
<=> \(\frac{500.9}{720} \leq k_2 \leq \frac{575.9}{720}\)
<=> \(6,25 \leq k_2 \leq 7,1875\)
=> \(k_2 = 7=> (1): \lambda_{lục} = 560nm.\)
720nm = 0,72 μm
giữa 2 vân sáng gần nhau nhất và cùng màu vs vân sáng trung tâm có 8 vân sáng màu lục => Tại vị trí trùng đó là VS bậc 9 của λlục
Tại VT trùng nhau: x_kđỏ = x_9lục
<=> kđỏ.λđỏ = 9.λlục
<=> kđỏ/9 = λlục/λđỏ = λ/0,72
=> λ = (0,72.kđỏ)/9 = 0,08.kđỏ (*)
0,5 ≤ λ = 0,08.kđỏ ≤ 0,575 μm
6,25 ≤ kđỏ ≤ 7,1875
=> kđỏ = 7
thế vào (*) λ = 0,56 (μm) = 560nm
đáp án : D
Đáp án B
Kể luôn 2 vân sáng trùng thì có 8 VS của λ2
=> có 7i2.
Gọi k là số khoảng vân của λ1 ;
Lúc đó ki1= 7i2 => kλ1= 7λ2
=> 0,67μm < λ2 = kλ1/7 < 0,74μm
=> 8,3 < k < 9,25 chọn k = 9
=> λ2 = 0,72μm
(Xét VS trùng gần VS TT nhất)
Khi 3 VS trùng nhau x1 = x2 = x3
Vị trí 3 VS trùng ứng với k1=9 , k2 = 7 , k3 = 12
Giữa hai Vân sáng trùng có 8 VS của λ1 ( k1 từ 1 đến 8)
6 VS của λ2 ( k2 từ 1 đến 6)
11 VS của λ3 ( k1 từ 1 đến 11)
Tổng số VS của 3 đơn sắc là 8+6+11= 25
Vì có 2 vị trí trùng của λ1 và λ3 ( với k1=3, k3=4 và k1=6, k3=8 )
nên số VS đơn sắc là 25 – 2= 23