Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A,B là 2 nguồn cùng pha nên đường trung trực của AB dao động cực đại.
Giữa M và đường trung trực của AB có 3 dãy dực đại khác => M nằm trên dãy cực đại k = 4
\(d_2-d_1=(k+\frac{\triangle\varphi}{2\pi})\lambda = (4+0)\lambda \Rightarrow \lambda = \frac{d_2-d_1}{4}=\frac{21-19}{4}=0.5cm \Rightarrow v = f.\lambda = 80.0,5=40cm/s.\)

Gọi hình chiếu của điểm M trên AB là N, trung điểm của AB là O, đặt ON = x \(\Rightarrow\) \(AM=\sqrt{4+\left(4-x\right)^2}\)\(,BM=\sqrt{4+\left(4+x\right)^2}\)
\(\vartheta BM=\frac{2\pi BM}{\lambda}\)
\(\vartheta AM=\frac{2\pi AM}{\lambda}\)
\(\Rightarrow\frac{2\pi}{\lambda}\left(MB-MA\right)=\left(2k+1\right)\lambda\pi\)
Min khi k = 0 \(\Leftrightarrow\sqrt{4+\left(4+x\right)^2}-\sqrt{4+\left(4-x\right)^2}\)\(=1\Rightarrow x\approx0,56\left(cm\right)\)
chọn đáp án A

2R < AB => số điểm dao động với biên độ lớn nhất trên (C) được tính như sau:
Số điểm dao động cực đại trên đoạn thẳng nối 2 nguồn (không tính hai nguồn) là
\(-AB < d_2-d_1< AB \Rightarrow -AB < (k+\frac{\triangle\varphi)}{2 \pi}\lambda< AB \\ \Rightarrow -AB/\lambda < k< AB/\lambda\\ \Rightarrow -3,062 < k < 3,062 \Rightarrow k = -3,-2,-1,0,1,2,3\)
=> Số điểm dao động với biên độ lớn nhất trên (C) là 7x2 = 14.



Đáp án: C
HD Giải: λ = v f = 30 20 = 1,5cm
Số điểm dao động cực đại trên đoạn CD thỏa mãn:
<=>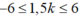
<=>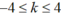
có 9 cực đại trên CD
Số cực đại trên đường tròn tâm O là 7.2 + 2 = 16