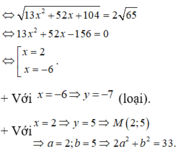Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương trình z 2 − z + 2017 2 = 0 ⇔ 4 z 2 − 4 z + 2017 = 0
⇔ 2 z − 1 2 = 2016 i 2 ⇔ z 1 = 1 − i 2016 2 z 2 = 1 + i 2016 2
Ta có z − z 1 + z − z 2 ≥ z − z 1 − z − z 2 = z − z 2 ≥ z 1 − z 2 − z − z 1 = 2016 − 1
Vật giá trị nhỏ nhất của biểu thức P là P min = 2016 − 1

Chọn đáp án C
Gọi M 1 , M 2 , M lần lượt là điểm biểu diễn của các số phức z 1 , 2 z 2 , z trên mặt phẳng tọa độ Oxy.
Do z 1 - 3 - 4 i = 1 nên quỹ tích điểm M 1 là đường tròn C 1 có tâm I 1 3 ; 4 và bán kính R = 1
Do z 2 - 3 - 4 i = 1 2 ⇔ 2 z 2 - 6 - 8 i = 1 nên quỹ tích điểm M 2 là đường tròn C 2 có tâm I 2 6 ; 8 và bán kính R = 2
Ta có điểm M(a; b) thỏa mãn 3a - 2b = 12 nên quỹ tích điểm M là đường thẳng d: 3x - 2y - 12 = 0
Khi đó
![]()
Gọi C 3 là đường tròn đối xứng với đường tròn C 2 qua đường thẳng d.
Ta tìm được tâm của C 3 là I 3 138 13 ; 64 13 và bán kính R = 1
Khi đó
![]()
với M 3 ∈ C 3 và A, B lần lượt là giao điểm của đường thẳng I 1 I 3 với hai đường tròn C 1 , C 3 (quan sát hình vẽ).
Dấu "=" xảy ra khi và chỉ khi M 1 ≡ A và M 3 ≡ B
Vậy P m i n = A B + 2 = I 1 I 3 = 3 1105 13

Chọn đáp án B.
Cách 1: (Sử dụng kiến thức Hình học)
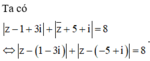
Gọi M, A, B, I lần lượt là điểm biểu diễn cho các số phức
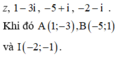
Có I là trung điểm của đoạn thẳng AB và

Áp dụng bất đẳng thức Cô-si, ta có


Cách 2: (Sử dụng kiến thức Đại số)
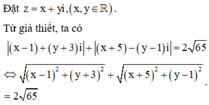
Áp dụng bất đẳng thức Bu-nhi-a-cốp-xky, ta có
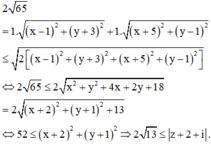
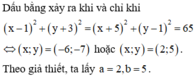


Đặt z = a + bi với a , b ∈ R
Khi đó
z - 2 i z - 2 = a + b - 2 i a - 2 + b i = a + b - 2 i a - 2 - b i a - 2 2 + b 2 = a a - 2 + b b - 2 a - 2 2 + b 2 + a - 2 b - 2 - a b a - 2 2 + b 2
z - 2 i z - 2 là số ảo khi và chỉ khi
a a - 2 + b b - 2 a - 2 2 + b 2 = 0 ⇔ a 2 + b 2 = 2 a + b a - 2 2 + b 2 ≠ 0
Ta có
P = z - 1 + z - i = a - 1 + b i + a + b - 1 i = a - 1 2 + b + a 2 + b - 1 2 = a 2 + b 2 - 2 a + 1 + a 2 + b 2 - 2 b + 1 = 2 a + b - 2 a + 1 + 1 a + b - 2 a + 1 = 1 + 2 b + 1 + 2
Áp dụng bất đẳng thức Cauchy ta có: 2 a + b = a 2 + b 2 ≥ 1 2 a + b 2
Suy ra a + b ≤ 4
Do đó P 2 ≤ 2 2 + 2 a + b ≤ 20 ⇔ P ≤ 2 5
Dấu “=” xảy ra khi và chỉ khi a = b = 2
Vậy maxP = 2 5 đạt được khi z = 2 + 2i
Đáp án C





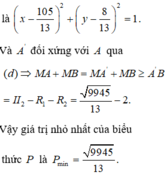
 bit lm bài này k giup tui
bit lm bài này k giup tui