Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án B
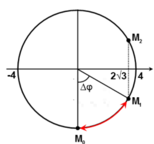
Ta biểu diễn vị trí ban đầu M 0 và vị trí dòng điện tức thời bằng 2 3 mA M 1 , M 2 trên đường tròn như hình vẽ. Dựa vào đường tròng, ta nhận thấy trong mỗi chu kì có 2 lần dòng điện có giá trị bằng 2 3 mA
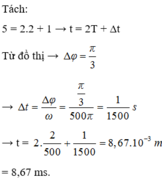

\(C = \frac{1}{\omega^2.L}= 5.10^{-6}F.\)
\(U_0 = \frac{q_0}{C}= \frac{I_0}{C.\omega}= \frac{I_0.\sqrt{L}}{\sqrt{C}} = 8V.\)
\(i = I = \frac{I_0}{\sqrt{2}}. \)
\(\left(\frac{u}{U_0}\right)^2+\left(\frac{i}{I_0}\right)^2=1\)
=> \(\left(\frac{u}{U_0}\right)^2 = 1- \left(\frac{i}{I_0}\right)^2 = 1 - \frac{1}{2}= \frac{1}{2}\)
=> \(u = \frac{1}{\sqrt{2}}U_0= 4\sqrt{2}V.\)

T=0.1
t2=t1+0.025=t1+T/4-->\(x_1^2+x_2^2=A^2\)-->x22=12
ma tai t1 dong giam va t2=t1+T/4 --->X2=-2\(\sqrt{3}\)

Mạch chỉ có điện trở thuần thì u cùng pha với i.
Nếu \(u=U_0\cos\left(\omega t+\varphi\right)\)
Thì: \(i=I_0\cos\left(\omega t+\varphi\right)\)
\(\Rightarrow\frac{u}{U_0}=\frac{i}{I_0}\)
\(\Rightarrow\frac{u^2}{U_0^2}+\frac{i^2}{I_0^2}=1\) là sai.

Sử dụng đường tròn
Từ thời điểm 0-0.01 s thì góc quay được là \(\varphi = 0.01.\omega = \pi (rad).\)
I 0 π/3 t=0 M N I 0 2 I 0 2 - t=0.01 P Q t 1 t 2 π/6 φ1 φ2
Thời điểm t =0 ứng với điểm M; thời điểm t = 0.01s ứng với điểm N. Từ M đến N sẽ qua hai điểm P và Q có giá trị (độ lớn) 0.5I0.
tại P: \(\varphi_1 = t_1 \omega => t_1 = \frac{\pi/3}{100\pi} = \frac{1}{300}s\)
tại Q: \(\varphi_2 = t_2 \omega => t_2 = \frac{\pi/3+\pi/6+\pi/6}{100\pi} = \frac{2}{300}s\)
chọn đáp án. A

Cách 1: Trong 5 μs = T/4 nên điện tích dịch chuyển là Q0
Số \( Ne = \frac{Q_0}{e} \text{ với } Q_0 = \frac{I_0}{\omega }\)
Đáp án A
Cách 2: Áp dụng \(q = n.e = \int_{0}^{5.10^{-6}} 0,012.\sin (10^5 \pi t) dt = 3,82.10^{-8}C \Rightarrow n = \frac{q}{e } = \frac{3,82.10^{-8}}{1,6.10^{-19}} = 2,39.10^{11}\)
Đáp án A
Chọn đáp án B
Ta biểu diễn vị trí ban đầu M 0 và vị trí dòng điện tức thời bằng 2 3 mA M 1 , M 2 trên đường tròn như hình vẽ. Dựa vào đường tròng, ta nhận thấy trong mỗi chu kì có 2 lần dòng điện có giá trị bằng 2 3 mA