Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn bị ngược rồi, B có 3 người còn A có 4 người mà. Không sao vẫn tính là bạn đang sắp xếp A nhé, mình kí hiệu 4 học sinh A là A1 A2 A3 A4 thì ở chỗ xếp học sinh A ấy bạn mới chỉ xếp cho A1, A2, A3 hoặc A4 mà thôi nên phải nhân 4 nữa. Đáp án phải là D
D.Công Thiện: Uh mình nhìn nhầm. Nhưng đáp án không thay đổi bạn ơi. Chỉ cần thay B bằng A thôi mà.

Xếp 6 học sinh trường A vào 1 dãy ghế: 6! cách
Xếp 6 học sinh trường B vào dãy còn lại: 6! cách
Lúc này hai học sinh đối diện luôn khác trường, có 6 cặp như vậy, mỗi cặp có 2 cách hoán vị nên có \(2^6\) cách hoán vị
Tổng cộng: \(6!.6!.2^6\) cách xếp thỏa mãn

a) Có 2 cách xếp.
Bạn A có 6! cách.
Bạn B có 6! cách.
Đổi vị trí A,B có tất cả 2*(6!)2 cách xếp chỗ.
b) Chọn 1 học sinh A vào vị trí bất kì: 12 cách.
Chọn 1 học sinh B đối diện A có 6 cách.
Cứ chọn liên tục như vậy ta được:
\(\left(12\cdot6\right)\cdot\left(10\cdot5\right)\cdot\left(8\cdot4\right)\cdot\left(6\cdot3\right)\cdot\left(4\cdot2\right)\cdot\left(2\cdot1\right)=2^6\cdot\left(6!\right)^2\)
cách xếp chỗ để hai bạn ngồi đối diện thì kkhasc trường nhau.

Chọn C
![]()
Ta có số phần tử không gian mẫu: Ω = 10!.
+) Có 10 cách chọn học sinh cho vị trí số 1. Với mỗi cách chọn vị trí số 1 có 5 cách chọn học sinh cho vị trí số 10 ( Nếu vị trí số 1 là học sinh X thì có 5 cách chọn học sinh ở vị trí 10 là học sinh Y và ngược lại).
+) Có 8 cách chọn học sinh cho vị trí số 2 ( Loại 2 học sinh ở vị trí 10) . Với mỗi cách chọn vị trí số 2 có 4 cách chọn học sinh cho vị trí số 9( Nếu vị trí số 2 là X thì có 4 cách chọn vị trí số 9 là Y, chỉ còn 4 do đã loại 1 em ở lần chọn trước).
+) Hoàn toàn tương tự cho đến hết ta được số phần tử của biến cố cần tính xác suất là: ![]()
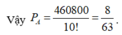
Đánh số 10 vị trí ngồi từ 1 đến 10 trong đó 1 đến 5 là hàng 1 thuộc bàn 1, còn 6 đến 10 là hàng 2 thuộc bàn 2.
Giả sử 1 học sinh trường X ngồi vị trí số 1, thì các học sinh còn lại của trường X chỉ ngồi ở vị trí số lẻ, còn 5 học sinh của trường Y chỉ ngồi vị trí số chẵn.
Số cách xếp lúc này là: 5!.5!. Tương tự với trường hợp học sinh trường X ngồi vị trí số chẵn.
vậy số cách xếp cần tìm: 2.5!.5! = 28800.
Chọn D.