Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Khi 1 ca sĩ hát thì mức cường độ âm là 68dB bạn ạ, bài này mình làm rồi.
Mình hướng dẫn này nhé:
Cách bạn giản ngắn nhưng vắn tắt quá. Theo giả thiết: $L_1=10log{\dfrac{I}{I_0}}=68dB \Rightarrow log{\dfrac{I}{I_0}}=6,8$
$ \Rightarrow \dfrac{I}{I_0}=10^{6,8}$(1)
$L_2=10log{\dfrac{nI}{I_0}}=80dB \Rightarrow log{\dfrac{I}{I_0}}=8$(2)
$ \Rightarrow n.\dfrac{I}{I_0}=10^{8}$
$ \Rightarrow n=\dfrac{10^8}{10^{6,8}}\approx 16$ (singers)
Khi mức cường độ âm tăng thêm 10n (dB) thì cường độ âm tăng thêm 10^n lần.
CM:
10lg(I2/I0) - 10lg(I1/I0) = 10n
=> lg(I2/I0) - lg(I1/I0) = n
=> lg(I2/I1) = n
=> I2/I1 = 10^n
=> I2 = 10^n.I1
Vậy khi mức cường độ âm nào đó tăng thêm 30dB thì cường độ của âm tăng lên 1000 lần.
Vậy B đúng
\(L=10log\frac{I}{I_0}\) Khi I tăng 1000 = 103 lần \(\Rightarrow\) L tăng 30 db
chọn B
Công thức tính mức cường độ âm là:
\(L=lg\frac{I}{I_0}=lg100=2B\) = 20 dB
Áp dụng công thức tính mức cường độ âm:
\(L\left(dB\right)=10.lg\frac{I}{I_0}=20dB\)
Gọi H là đường chân cao hạ từ O đến MN
Giả sử OH = 1 → OM \(=\sqrt[4]{10};ON=\sqrt{10}\)
Do đó tính \(\widehat{MON}\approx1270,35^o\)
A đúng
Đáp án D
+ Ta có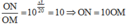 
, chuẩn hóa
→ Trung điểm I của MN cách MN một đoạn 4,5
→ Mức cường độ âm tại M khi đi đặt nguồn âm tại I:
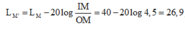dB
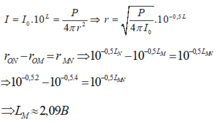
Đáp án B
Ta có L2 – L1 = 10lg(P2/P1) = 10lg20 = 13dB
→ L2 = L1 + 13 = 58dB.