Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

d : { x = 1 - t y = 2 + 2 t z = 3 + t có 1 véc tơ chỉ phương là u → - 1 ; 2 ; 1 và P : x - y + 3 = 0 có véc tơ pháp tuyến là n → 1 , - 1 , 0
Khi đó : góc giữa đường thẳng d và mặt phẳng (P) là:
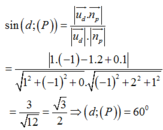
Chọn A.

Lời giải:
a) Gọi phương trình đường thẳng có dạng $y=ax+b$ $(d)$
Vì \(B,C\in (d)\Rightarrow \left\{\begin{matrix} 3=2a+b\\ -3=-4a+b\end{matrix}\right.\Rightarrow \left\{\begin{matrix} a=1\\ b=1\end{matrix}\right.\Rightarrow y=x+1\)
Vậy PT đường thẳng chứa cạnh $BC$ có dạng $y=x+1$
b) Tương tự, ta lập được phương trình đường thẳng chứa cạnh $AC$ là \((d_1):y=\frac{2x}{5}-\frac{7}{5}\).
Gọi PT đường cao đi qua $B$ của tam giác $ABC$ là \((d'):y=ax+b\)
Vì \((d')\perp (d_1)\Rightarrow \frac{2}{5}a=-1\Rightarrow a=\frac{-5}{2}\).
Mặt khác \(B\in (d')\Rightarrow 3=\frac{-5}{2}.2+b\Rightarrow b=8\)
\(\Rightarrow (d'):y=\frac{-5x}{2}+8\)
c) Gọi điểm thỏa mãn ĐKĐB là $M(a,b)$
Ta có: \(M\in (\Delta)\Rightarrow 2a+b-3=0\) $(1)$
$M$ cách đều $A,B$ \(\Rightarrow MA^2=MB^2\Rightarrow (a-1)^2+(b+1)^2=(a-2)^2+(b-3)^2\)
\(\Leftrightarrow 2-2a+2b=13-4a-6b\)
\(\Leftrightarrow 11-2a-8b=0(2)\)
Từ \((1);(2)\Rightarrow \left\{\begin{matrix} a=\frac{13}{14}\\ b=\frac{8}{7}\end{matrix}\right.\Rightarrow M\left ( \frac{13}{14};\frac{8}{7} \right )\)
con nếu đề bài cho 1 điểm và phương trình đường thẳng của tam giác muốn tìm phương trình đường cao còn lại vầ các cạnh thj làm thế nào

a) Ta có: góc FAB + góc BAC = 90 độ
góc EAC + góc BAC = 90 độ
=> Góc FAB = góc EAC
AF=AC; AB=AE
=> Tam giác AFB = tam giác ACE
=> FB=EC
b) Lấy K sao cho M là trung điểm của AK thì ta có ACKB là hình bình hành nên góc ACB =180* - góc BAC. Ta cũng tính dc góc FAE= 180* - góc BAC ( tổng của BAC với 2 lần góc CAE, mà góc CAE=90* -góc BAC). Thêm với AC=AF , CK=AE (=AB) nên tam giác ACK = tam giác FAE nên AK=EF mà AK=2AM nên EF=2AM
c) Gọi H là giao của AM và EF. Tam giác ACK = tam giác FAE nên góc CAK = góc AFE, mà góc CAK phụ với góc MAF nên góc AFE cũng phụ góc MAF. Xét trong tam giác AHF có góc F và góc A phụ nhau nên tam giác AHF vuông tại H suy ra AM vuông góc với EF.

Ta có Pt d2 :x+2y-5=0
vì M ϵ d1 :x-y-1=0 nên M(m,m-1)
MA2 = (-1-m)2 + (2-m+1)2 = 1+2m+m2 +9-6m+m2 =2m2 -4m+10
<=> MA=\(\sqrt{2m^2-4m+10}\)
d(m,d2 )= \(\frac{\left|m+2m-2-5\right|}{\sqrt{1^2+2^2}}\) =\(\frac{\left|3m-7\right|}{\sqrt{5}}\)
theo bài ra thì MA=d(M,d2)
=>\(\frac{\left|3m-7\right|}{\sqrt{5}}\)=\(\sqrt{2m^2-4m+10}\) <=>|3m-7|=\(\sqrt{5}\)\(\sqrt{2m^2-4m+10}\)
<=>9m2 -42m +49=5(2m2-4m+10)
<=>9m2 -42m +49=10m2 -20m +50
<=>m2 +22m +1=0
<=>m= -11+2\(\sqrt{30}\) hoặc m=-11-2\(\sqrt{30}\)
=> M(-11+2\(\sqrt{30}\) ,-12+2\(\sqrt{30}\) ) hoặc M(-11-2\(\sqrt{30}\) ,-12-2\(\sqrt{30}\) )

Chọn D.
Phương pháp: Tính thông qua góc giữa các véc tơ chỉ phương và pháp tuyến của đường thẳng và mặt phẳng đó.


Chọn A
Tìm giao điểm I từ hệ phương trình đường thẳng d và mặt phẳng (P). Viết phương trình đường thẳng IM. Gọi tọa độ điểm M theo tham số của đường thẳng IM rồi xác định tham số đó từ phương trình I M = 4 14

Gọi φ là góc giữa đường thẳng d và mặt phẳng (P).
Ta có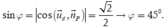
Chọn B.