Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
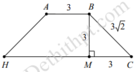
Ta có:
A B → = 2 ; 1 ; − 2 A C → = 6 ; 0 ; − 3 ⇒ A B → ; A C → = 3 ; 6 ; 6 ⇒ d C ; A B = A B → ; A C → A B → = 3
Gọi M là hình chiếu của B trên H C ⇒ B M = 3.
Tam giác BMC vuông tại M, có M C = B C 2 − B M 2 = 3
Suy ra
H C = A B + 2. M C = 3 + 2.3 = 9 = 3 A B ⇒ C H → = 3 B A →
Mà B A → = − 2 ; − 1 ; 2 C H → = x − 5 ; y ; z + 2
suy ra x = 5 = 3. − 2 y = 3. − 1 z + 2 = 3.2 ⇔ x = − 1 y = − 3 z = 4
Vậy H − 1 ; − 3 ; 4 .

Chọn C.
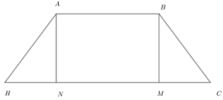
Phương pháp: Sử dụng các véc tơ bằng nhau.

Giả sử M,N lần lượt là hình chiếu của A, B lên CH.

Vì ABCD là hình thang cân nên AD = BC = 3.
Gọi ∆ là đường thẳng qua C và song song với AB.
Gọi (S) là mặt cầu tâm A bán kính R = 3. Điểm D cần tìm là giao điểm của ∆ và (S).
Đường thẳng ∆ có vectơ chỉ phương A B → - 2 ; 6 ; 3 nên có phương trình:
x = 2 - 2 t y = 3 + 6 t z = 3 + 3 t
Phương trình mặt cầu
S : x - 3 2 + y + 1 2 + z + 2 2 = 9 .
Tọa độ điểm D là nghiệm của phương trình
- 2 t - 1 2 + 6 t + 4 2 + 3 t + 5 2 = 9 ⇔ 49 t 2 + 82 t + 33 = 0 ⇔ t = - 1 t = - 33 49 .
Đáp án B

Đáp án là B
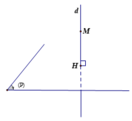
Phương trình đường thẳng d đi qua M vuông góc
với (P) nhận véc tơ pháp tuyến



Đáp án C