Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
Ta có log x a = 1 α ; log x b = 1 β ; log x c = 1 γ
⇒ log x a + log x b + log x c = 1 α + 1 β + 1 γ ⇒ log x a b c = α β + β γ + γ α α β γ
⇔ log a b c x = α β γ α β + β γ + γ α .

ta có \(y=\frac{3\left(x+1\right)}{x-2}=3+\frac{9}{x-2}\) để các điểm trên C có tọa độ nguyên thì (x,y) nguyên
suy ra (x-2) là ước của 9
mà \(Ư\left\{9\right\}=\left\{\pm9;\pm3;\pm1\right\}\)
TH1: x-2=-9 suy ra x=-7 suy ra y=3-1=2
th2: x-2=9 suy ra x=11 suy ra y=3+1=4
th3:x-2=-3 suy ra x=-2 suy ra y=3-3=0
th4: x-2=3 suy ra x=5 suy ra y=3+3=6
th5:x-2=1 suy ra x=3 suy ra y=3+9=12
th6: x-2=-1 suy ra x=1 suy ra y=3-9=-6
kết luận....

Đáp án D
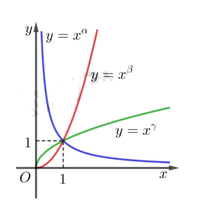
Hàm số x α nghịch biến do đó 0 < α < 1 .
Các hàm số x β , x γ là các hàm số đồng biến do đó β , γ > 1 .
Cho x = 100 ⇒ 100 β > 100 γ ⇒ β > γ .

Đáp án D
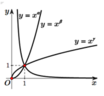
Với x > 1 mà lim x α = 0 ⇔ 0 < a < 1 và cũng suy ra β , γ > 1
Với x > 1 , với cùng 1 giá trị x 0 thì x β > x γ ⇒ β > γ .

hoành độ giao điểm là nghiệm của pt
\(x^3+3x^2+mx+1=1\Leftrightarrow x\left(x^2+3x+m\right)=0\)
\(x=0;x^2+3x+m=0\)(*)
để (C) cắt y=1 tại 3 điểm phân biệt thì pt (*) có 2 nghiệm phân biệt khác 0
\(\Delta=3^2-4m>0\) và \(0+m.0+m\ne0\Leftrightarrow m\ne0\)
từ pt (*) ta suy ra đc hoành độ của D, E là nghiệm của (*)
ta tính \(y'=3x^2+6x+m\)
vì tiếp tuyến tại Dvà E vuông góc
suy ra \(y'\left(x_D\right).y'\left(x_E\right)=-1\)
giải pt đối chiếu với đk suy ra đc đk của m

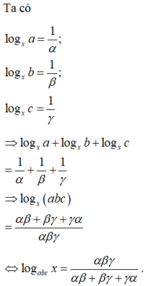
 bit lm bài này k giup tui
bit lm bài này k giup tui
Chọn đáp án B.