Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Phương pháp: Giả sử đường thẳng (d) cắt trục Oz tại điểm ![]()
Cách giải:
Giả sử đường thẳng (d) cắt trục Oz tại điểm ![]()
![]()
![]()
![]()
![]()
![]()

![]() có VTCP là
có VTCP là ![]()
Mặt phẳng (P) có VTCP ![]()
Theo giả thiết d//(P) nên suy ra ![]()
![]()
Vậy đường thẳng d có một VTCP ![]()
nên loại các phương án A, C, D.
Chọn B.

Đáp án A
Vì M ∈ d nên M t + 3 ; − t − 2 ; 2 t + 1 , t ∈ ℝ
Đường thẳng Δ có vtcp u Δ → = − 1 ; 2 ; − 3 .
Đường thẳng d ' : qua M t + 3 ; − t − 2 ; 2 t + 1 vtcp u d ' → = u Δ → = − 1 ; 2 ; − 3
⇒ d ' : x − t + 3 − 1 = y + t + 2 2 = z − 2 t + 1 − 3
M’ là hình chiếu song song của M trên (P)
⇒ M ' = d ' ∩ P ⇒ M ' 5 9 t + 2 ; − 1 9 t ; 2 3 t − 2 .
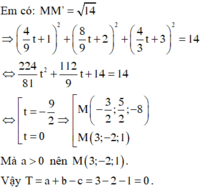

Đường thẳng d đi qua A ( 1;-1;2 ) có vec tơ chỉ phương u → ( a ; b ; c ) do d song song (P): 2x - y - z + 3 = 0 nên u → ( a ; b ; c ) ⊥ n ( 2;-1;1 )
⇔ u → . n = 0 ⇔ 2a = b + c
Đến đây ta kiểm tra chỉ có đáp án A là đường thẳng có véc tơ chỉ phương thỏa mãn (1) nên ta chọn đáp án A
Đáp án cần chọn là A

Đáp án B.
Dễ thấy d ⊥ α và − 1 ; − 2 ; − 3 ∈ α ⇒ d ⊂ α .
Ta có B = Δ ∩ Oxy ⇒ B a ; b ; 0 mà B ∈ Δ ⊂ α ⇒ 2 a + b − 2 = 0 (1).
Lại có d / / Δ ⇒ d d ; Δ = d B ; d = 3.
Đường thẳng d đi qua M 0 ; 0 ; − 1 , có u d → = 1 ; 2 ; 2 .
Do đó:
d B ; d = B M → ; u d → u d → = 2 b − 2 2 + 1 − 2 a 2 + 2 a − b 2 3 = 3 2
Từ (1), (2) suy ra:
a ; b = − 1 ; 4 → B − 1 ; 4 ; 0 a ; b = 2 ; − 2 → B 2 ; − 2 ; 0 .
Vậy A B = 7 2 .


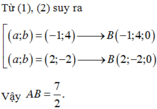

Đường thẳng d có vectơ chỉ phương u → 2 ; - 3 ; 1 , qua H ( -2;4;-1 )
Mặt phẳng (P) có vectơ pháp tuyến n → A ; B ; C ; A 2 + B 2 + C 2 > 0
Ta có
d / / P ⇔ u → . n → = 0 H - 2 ; 4 ; - 1 ∉ P ⇔ 2 A - 3 B + C = 0 - 3 A + 4 B - C ≠ 0 ⇔ C = 0 - 2 A + 3 B C ≠ 3 A - 4 B
Mặt khác (P) qua K ( 1;0;0 ) suy ra P : A x + B y + 3 B - 2 A z - A = 0
Ngoài ra
d M ; P = - 5 A + 8 B A 2 + B 2 + 3 B - 2 A 2 = 3 ⇔ 5 A 2 - 22 . A B + 17 B 2 = 0 ⇔ A = B 5 A = 17 B
Với A = B ⇒ C = B không thỏa mãn (*)
Với 5A = 17B, chọn A = 17, suy ra B = 5, do đó C = -19 (nhận)
Vậy (P): 17x + 5y - 19z - 17 = 0
Đáp án B