
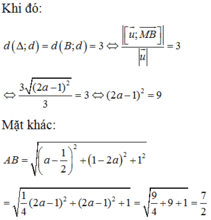
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


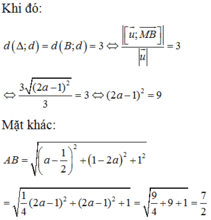

Đáp án B
Phương pháp:
![]()
![]()
![]()
thay tọa độ điểm B vào phương trình ( α ) => 1 phương trình 2 ẩn a, b.
![]()
Sử dụng công thức tính khoảng cách
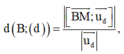
lập được 1 phương trình 2 ẩn chứa a, b.
+) Giải hệ phương trình tìm a,b => Toạ độ điểm B => Độ dài AB.
Dế thấy
![]()
Ta có
![]()
![]()
![]()
Lại có
![]()
Đường thẳng d đi qua M(0;0;-1), có u → = ( 1 ; 2 ; 2 )
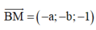
![]()
Do đó
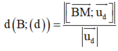
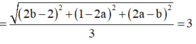
![]()
![]()
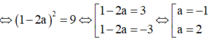
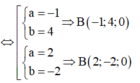
Vậy AB = 7 2

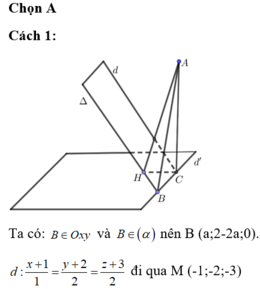
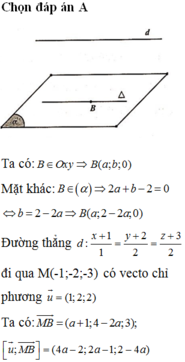
Ta có: d ⊂ (α) nên d và ∆ song song với nhau và cùng nằm trong mặt phẳng (α).
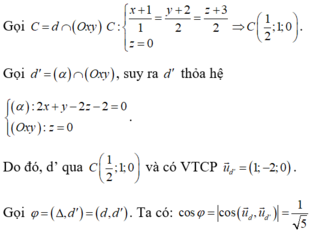


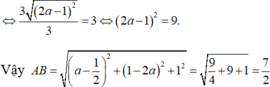

Chọn A
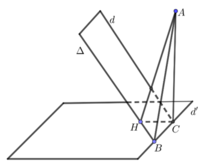
Cách 1: Ta có: B ∈ Oxy và B ∈ (α) nên B (a ; 2 – 2a ; 0).
![]() đi qua M (-1 ; -2 ; -3) và có một véctơ chỉ phương là
đi qua M (-1 ; -2 ; -3) và có một véctơ chỉ phương là ![]()
Ta có: d ⊂ (α) nên d và Δ song song với nhau và cùng nằm trong mặt phẳng (α).
Gọi C = d ∩ (Oxy) nên 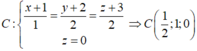
Gọi d’ = (α) ∩ (Oxy), suy ra d’ thỏa hệ 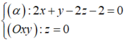
Do đó, d’ qua 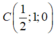 và có VTCP
và có VTCP ![]()
Gọi φ = (Δ, d’) = (d, d’)
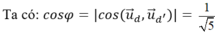
Gọi H là hình chiếu của C lên Δ. Ta có CH = 3 và 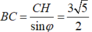
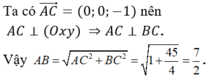
Cách 2: Ta có: ![]() đi qua M (-1 ; -2 ; -3) và có một VTCP là
đi qua M (-1 ; -2 ; -3) và có một VTCP là ![]()
Ta có: B = Δ ∩ (Oxy), Δ ⊂ (α) nên B ∈ (Oxy) ∩ (α) => B (a; 2 – a; 0)
Ta có: Δ // d và d (Δ, d) = 3 nên 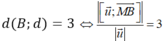

B C A D H K J S
Kẻ \(SH\perp AC\left(H\in AC\right)\)
Do \(\left(SAC\right)\perp\left(ABCD\right)\Rightarrow SH\perp\left(ABCD\right)\)
\(SA=\sqrt{AC^2-SC^2}=a;SH=\frac{SA.SC}{AC}=\frac{a\sqrt{3}}{2}\)
\(S_{ABCD}=\frac{AC.BD}{2}=2a^2\)
\(V_{S.ABCD}=\frac{1}{3}SH.S_{ABCD}=\frac{1}{3}.\frac{a\sqrt{3}}{2}.2a^2=\frac{a^3\sqrt{3}}{3}\)
Ta có \(AH=\sqrt{SA^2-SH^2}=\frac{a}{2}\Rightarrow CA=4HA\Rightarrow d\left(C,\left(SAD\right)\right)=4d\left(H,\left(SAD\right)\right)\)
Do BC//\(\left(SAD\right)\Rightarrow d\left(B,\left(SAD\right)\right)=d\left(C,\left(SAD\right)\right)=4d\left(H,\left(SAD\right)\right)\)
Kẻ \(HK\perp AD\left(K\in AD\right),HJ\perp SK\left(J\in SK\right)\)
Chứng minh được \(\left(SHK\right)\perp\left(SAD\right)\) mà \(HJ\perp SK\Rightarrow HJ\perp\left(SAD\right)\Rightarrow d\left(H,\left(SAD\right)\right)=HJ\)
Tam giác AHK vuông cân tại K\(\Rightarrow HK=AH\sin45^0=\frac{a\sqrt{2}}{4}\)
\(\Rightarrow HJ=\frac{SH.HK}{\sqrt{SH^2+HK^2}}=\frac{a\sqrt{3}}{2\sqrt{7}}\)
Vậy \(d\left(B,\left(SAD\right)\right)=\frac{2a\sqrt{3}}{\sqrt{7}}=\frac{2a\sqrt{21}}{7}\)

Đáp án B
![]()
![]()
Vì M là hình chiếu vuông góc của I trên ∆
![]()
Khi đó
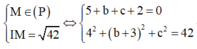
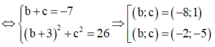
Vậy M(5;-2;-5) hoặc M(5;-8;1) => bc =10

Chọn C
Phương trình tham số của đường thẳng 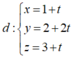
I ∈ d => I (1+t;2+2t;3+t)
I ∈ (α) => 1 + t + 2 + 2t – (3 + t) -2 = 0 ó t = 1 => I (2;4;4).

Đường thẳng cần tìm qua điểm I (2;4;4), nhận một VTCP là ![]() nên có PTTS
nên có PTTS 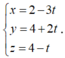
Kiểm tra ![]() , thấy A (5;2;5) thỏa mãn phương trình (*). Vậy chọn C.
, thấy A (5;2;5) thỏa mãn phương trình (*). Vậy chọn C.