Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mặt phẳng gọi là (P) đi cho dễ gõ kí tự.
Thay tọa độ A; B vào (P) cho 2 kết quả cùng dấu dương \(\Rightarrow\) A và B nằm cùng phía so với (P)
Gọi A' là điểm đối xứng với A qua (P), với điểm M bất kì thuộc (P) ta luôn có \(MA=MA'\Rightarrow MA+MB=MA'+MB\ge A'B\)
\(\Rightarrow MA+MB_{min}\) khi M;B;A' thẳng hàng hay M là giao điểm của đường thẳng A'B và (P)
Pt tham số của đường thẳng d qua A và vuông góc (P) nhận \(\left(1;-2;0\right)\) là vtcp: \(\left\{{}\begin{matrix}x=1+t\\y=-2t\\z=-2\end{matrix}\right.\)
Gọi C là giao của d và (P) \(\Rightarrow\) tọa độ C thỏa mãn:
\(1+t-2\left(-2t\right)+11=0\Rightarrow t=-\frac{12}{5}\) \(\Rightarrow C\left(-\frac{7}{5};\frac{24}{5};-2\right)\)
C là trung điểm AA' \(\Rightarrow A'\left(-\frac{19}{5};\frac{48}{5};-2\right)\)
\(\Rightarrow\overrightarrow{A'B}=\left(\frac{24}{5};-\frac{43}{5};-3\right)=\frac{1}{5}\left(24;-43;-15\right)\)
Phương trình tham số A'B: \(\left\{{}\begin{matrix}x=1+24t\\y=1-43t\\z=-5-15t\end{matrix}\right.\)
Tọa độ M thỏa mãn:
\(1+24t-2\left(1-43t\right)+11=0\Rightarrow t=-\frac{1}{11}\) \(\Rightarrow M\left(-\frac{13}{11};\frac{54}{11};-\frac{40}{11}\right)\)
Kết quả ko giống, bạn xem lại đề bài có ghi nhầm chỗ nào ko


Gọi I là trung điểm của đoạn thẳng AB. Khi đó \(I\left(2;0;2\right)\) với mọi điểm M đều có :
\(MA^2+MB^2=\overrightarrow{MA^2}+\overrightarrow{MB^2}\)
\(=\left(\overrightarrow{MI}+\overrightarrow{IA}\right)^2+\left(\overrightarrow{MI}+\overrightarrow{IB}\right)^2\)
\(=2MI^2+\left(IA^2+IB^2\right)=2MI^2+\frac{AB^2}{2}\)
Do đó \(M\in\left(P\right)\) sao cho \(MA^2+MB^2\) bé nhất khi và chỉ khi M là hình chiếu của I trên mặt phẳng (P)
Gọi \(\left(x;y;z\right)\) là tọa độ hình chiếu vuông góc của điểm I trên mặt phẳng (P). Khi đó ta có hệ phương trình :
\(\begin{cases}x+y+z-6=0\\\frac{x-2}{1}=\frac{y-0}{1}=\frac{z-2}{1}\end{cases}\)
Giải hệ thu được :
\(x=\frac{8}{3};y=\frac{2}{3};z=\frac{8}{3}\)
Vậy điểm M cần tìm là \(M\left(\frac{8}{3};\frac{2}{3};\frac{8}{3}\right)\)

câu 5 ấy chắc thầy tui buồn ngủ nên quánh lộn chữ sai thành đúng r
12.
\(R=d\left(I;Oxz\right)=\left|y_I\right|=3\)
Phương trình:
\(x^2+\left(y+3\right)^2+z^2=9\)
\(\Leftrightarrow x^2+y^2+z^2+6y=0\)
13.
\(R=d\left(M;\alpha\right)=\frac{\left|1-1+2.2-3\right|}{\sqrt{1^2+1^2+2^2}}=\frac{1}{\sqrt{6}}\)
Pt mặt cầu:
\(\left(x-1\right)^2+\left(y-1\right)^2+\left(z+2\right)^2=\frac{1}{6}\)
14.
\(R=d\left(I;\left(P\right)\right)=\frac{\left|-1-4-2-2\right|}{\sqrt{1^2+2^2+2^2}}=3\)
Phương trình:
\(\left(x+1\right)^2+\left(y-2\right)^2+\left(z-1\right)^2=9\)
\(\Leftrightarrow x^2+y^2+z^2+2x-4y-2z-3=0\)

19.
Phương trình mặt phẳng theo đoạn chắn:
\(\frac{x}{3}+\frac{y}{-4}+\frac{z}{-2}=1\)
\(\Leftrightarrow4x-3y-6z-12=0\)
20.
Phương trình mặt phẳng (ABC) theo đoạn chắn:
\(\frac{x}{1}+\frac{y}{2}+\frac{z}{3}=1\)
\(\Leftrightarrow6x+3y+2z-6=0\)
Chẳng đáp án nào đúng cả, chắc bạn ghi nhầm đáp án C số 1 thành số 0 :)
15.
\(2\left(x-2\right)-5\left(y+3\right)+1\left(z+2\right)=0\)
16.
\(\overrightarrow{n_1}=\left(1;1;-1\right)\) ; \(\overrightarrow{n_2}=\left(1;-1;1\right)\)
\(\left[\overrightarrow{n_1};\overrightarrow{n_2}\right]=\left(0;-2;-2\right)=-2\left(0;1;1\right)\)
Phương trình (P):
\(1\left(y-1\right)+1\left(z-1\right)=0\Leftrightarrow y+z-2=0\)
17.
\(\overrightarrow{n_P}=\left(1;-1;1\right)\) ; \(\overrightarrow{n_Q}=\left(3;2;-12\right)\)
\(\left[\overrightarrow{n_P};\overrightarrow{n_Q}\right]=\left(10;15;5\right)=5\left(2;3;1\right)\)
Phương trình mặt phẳng (R):
\(2x+3y+z=0\)
18.
\(\overrightarrow{MN}=\left(0;-2;3\right);\overrightarrow{MP}=\left(-2;1;3\right)\)
\(\left[\overrightarrow{MN};\overrightarrow{MP}\right]=\left(-9;-6;-4\right)=-1\left(9;6;4\right)\)
Phương trình:
\(9\left(x-2\right)+6\left(y-2\right)+4z=0\)
\(\Leftrightarrow9x+6y+4z-30=0\)

\(\overrightarrow{AB}=\left(-1;-2;1\right)\); \(\overrightarrow{n_{\alpha}}=\left(2;-1;2\right)\)\(\Rightarrow\overrightarrow{n_p}=\left[\overrightarrow{AB};\overrightarrow{n_{\alpha}}\right]=\left(-3;4;5\right)\)
Phương trình mặt phẳng (P) : \(-3x+4y+5z=0\)
\(R=d\left(A;\left(\alpha\right)\right)=\frac{\left|6-1+2+1\right|}{\sqrt{9}}=\frac{8}{3}\)
Phương trình mặt cầu (S) : \(\left(x-3\right)^2+\left(y-1\right)^2+\left(z-1\right)^2=\frac{64}{9}\)
Chọn D
Gọi G (2;2;-2) là trọng tâm tam giác ABC, khi đó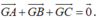
Ta có:
đạt giá trị nhỏ nhất khi M là hình chiếu vuông góc của G trên mặt phẳng (P). Khi đó tọa độ của M (a;b;c) và vecto cùng phương với vecto pháp tuyến n (1;-2;2) thỏa mãn hệ
cùng phương với vecto pháp tuyến n (1;-2;2) thỏa mãn hệ 
Vậy a+b+c=3.